Project 1: Problem 7 Posted on January 29
Main PageDescription
Now we will clamp both ends of our beam and use a sinusoidal force (sinusoidalforces.m). The structure of our initial matrix is altered slightly in initclampedmatrix.m so that the final 2 rows are the reverse of the first two rows. Our errors are obtained through Problem 7 and are as follows for \(x=\frac{L}{2}\) against the correct solution, \[ y(x)=\frac{f}{24EI}x^2(L-x)^2-\frac{pgL^2}{\pi^4EI}(L^2\sin\frac{\pi}{L}x+\pi x(x-L)). \]
| \(n\) | Error | Condition Number |
|---|---|---|
| 10 | 0.001668593932958 | 805 |
| 20 | 0.000797116989074 | 10652 |
| 40 | 0.000389529641042 | 154595 |
| 80 | 0.000192541455493 | 2354357 |
| 160 | 0.000095718910114 | 36745380 |
| 320 | 0.000047721984204 | 580645427 |
| 640 | 0.000023826669975 | 9232533524 |
| 1280 | 0.000011904768050 | 147259976987 |
| 2560 | 0.000005949391567 | 2352479784190 |
| 5120 | 0.000002949775262 | 37610490062507 |
| 10240 | 0.000001865160826 | 601604110154096 |
| 20480 | 0.000001600275175 | 9615665665490997 |
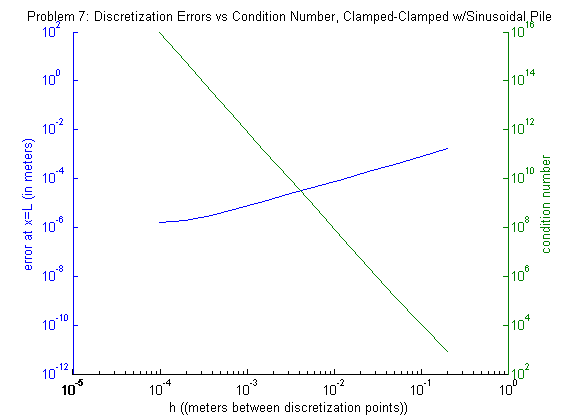
This table implies that our error has a linear relationship to \(n\) but the condition number does not come into play as it did in Problem 5. The following plot exhibits this relationship:
The error (blue) seems to be concave up as \(n\) increase (\(h\) decreases) which suggests that the condition number may begin to have a significant effect if we tested higher values of \(n\). This plot also shows that the error is approximately proportional to \(h^2\) as claimed in the description. To get a picture of the beam itself, we modified our code a bit to problem7deflection.m:
This concludes our first project of MATH 447 Numerical Analysis II under Dr. Tim Sauer. We hope you enjoyed reading about our investigations. You may return to the project's main page here. Please download the code and try it yourself!
<< PreviousRelated posts
Problem 1
Basic initialization of matrix with \(n=10\)
Problem 2
Comparison of solution obtained in Problem 1 and the theoretical solution
Problem 3
Similar problem for various values of \(n\)
Problem 4
Theoretical exercise for sinusoidal pile
Problem 5
Addition of sinusoidal load for various values of \(n\)
Problem 6
Replacing sinusoidal load with 70 kg diver
Problem 7
Clamped-clamped model with a sinusoidal load