Project 1: Problem 6 Posted on January 29
Main PageDescription
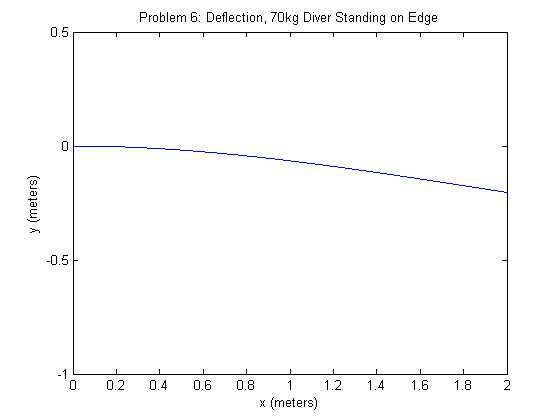
Here we add a 70 kg diver to the final 20 cm of our beam. Our force per unit length is \(-g \cdot \frac{70}{0.2}\). We will solve this system for \(n=1280\), which was the optimal value for Problem 5. We plot the solution below (using problem6.m, initmatrix.m, and diverforces.m).
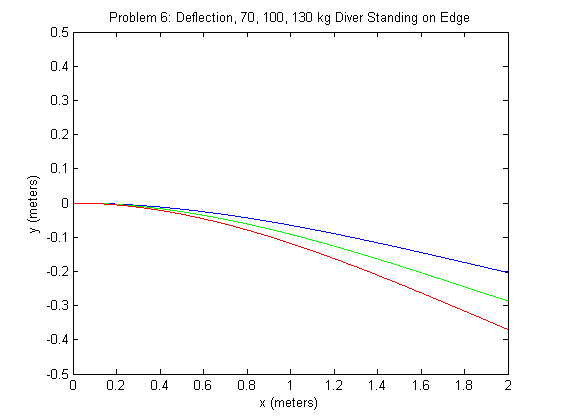
Our deflection at \(x=2m\) is -0.203411003731169. Additionally, we plot the solution for diver weights of 70, 100, 130 kg in blue, green, and red, respectively:
This second plot confirms intuition that heavier divers would cause more deflection in the beam. Finally we will solve for the deflection on the beam under a sinusoidal force when both ends of the beam are clamped in Problem 7.
<< Previous Next >>Related posts
Problem 1
Basic initialization of matrix with \(n=10\)
Problem 2
Comparison of solution obtained in Problem 1 and the theoretical solution
Problem 3
Similar problem for various values of \(n\)
Problem 4
Theoretical exercise for sinusoidal pile
Problem 5
Addition of sinusoidal load for various values of \(n\)
Problem 6
Replacing sinusoidal load with 70 kg diver
Problem 7
Clamped-clamped model with a sinusoidal load