Project 1: Problem 2 Posted on January 29
Main PageHere we are tasked with comparing our calculated solution from Problem 1 against the correct solution \( y(x) = (\frac{f}{24EI})x^2(x^2-4Lx+6L^2) \). We will do this primarily through a graphical comparison but will provide a numerical result as well.
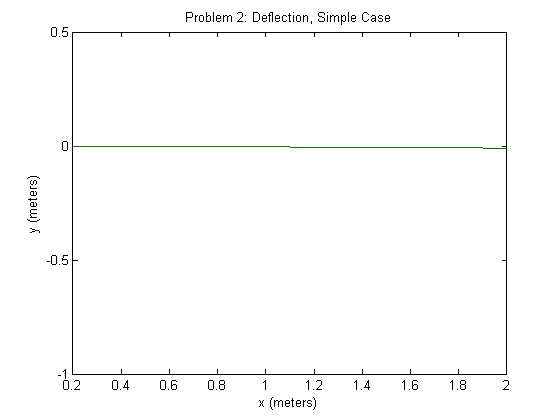
Using the code in problem2.m, we obtained a numerical error result of 6.609296443471653e-16 at \(x=2m\). As expected, this numerical result is close to machine roundoff since our derivative approximations are exact. Below we showcase a plot of our calculated solution (blue) against the correct solution (green). As you can see, the two solutions are indistinguishable to the eye and that, under only its own weight, the beam's deflection at 2 meters is small.
We will now proceed to analyze our calculated solutions for various discretization widths in Problem 3
<< Previous Next >>Related posts
Problem 1
Basic initialization of matrix with \(n=10\)
Problem 2
Comparison of solution obtained in Problem 1 and the theoretical solution
Problem 3
Similar problem for various values of \(n\)
Problem 4
Theoretical exercise for sinusoidal pile
Problem 5
Addition of sinusoidal load for various values of \(n\)
Problem 6
Replacing sinusoidal load with 70 kg diver
Problem 7
Clamped-clamped model with a sinusoidal load