Project 1: Problem 3 Posted on January 29
Main PageWe will now generalize our procedure from Problem 2 for values of \( n = 10 \cdot 2^k \) with \( k = 1, \dots, 11 \). Our errors versus the solution are as follows:
| \(n\) | Error | Condition Number |
|---|---|---|
| 10 | 0.000000000000661e-03 | 33300 |
| 20 | 0.000000000004058e-03 | 530300 |
| 40 | 0.000000000196865e-03 | 8449300 |
| 80 | 0.000000001338461e-03 | 134821300 |
| 160 | 0.000000015524033e-03 | 2153877300 |
| 320 | 0.000000374602927e-03 | 34434645700 |
| 640 | 0.000000820345836e-03 | 550730051100 |
| 1280 | 0.000004269560688e-03 | 8809863858700 |
| 2560 | 0.000170064631584e-03 | 140942917022200 |
| 5120 | 0.003796953486315e-03 | 2254930318385600 |
| 10240 | 0.039358200510426e-03 | 36175997867570800 |
| 20480 | 0.496388138887950e-03 | 615713526613343200 |
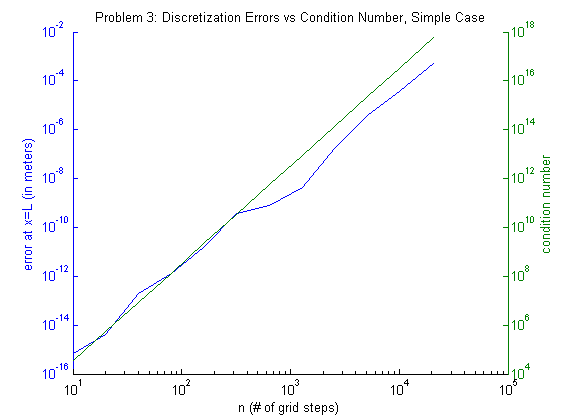
This table shows that our error is the smallest when \(n=10\) and scales linearly with the condition number of our matrix \(A\). Graphically, it can be seen that the error-condition number relationship is linear under our constat force assumptions. This makes sense because, as we showed previously, our error is very close to machine roundoff already. Hence, we cannot expect to do better with more discretization steps. In fact, we expect to do worse because of the accumulation of roundoff errors. The following plot shows the errors (left-blue axis) and the condition number (right-green axis). The relationship is almost perfectly linear over the entire range.
Our next task is to add a sinusoidal pile, i.e. \(s(x) = -pg\sin\frac{\pi}{L}x\), and prove that the solution to this problem is:
\(y(x)=\frac{f}{24EI}x^2(x^2-4Lx+6L^2)-\frac{pgL}{EI\pi}(\frac{L^3}{\pi^3}\sin{\pi}{L}x - \frac{x^3}{6}+\frac{L}{2}x^2-\frac{L^2}{\pi^2}x) \)
This is done in Problem 4.
<< Previous Next >>Related posts
Problem 1
Basic initialization of matrix with \(n=10\)
Problem 2
Comparison of solution obtained in Problem 1 and the theoretical solution
Problem 3
Similar problem for various values of \(n\)
Problem 4
Theoretical exercise for sinusoidal pile
Problem 5
Addition of sinusoidal load for various values of \(n\)
Problem 6
Replacing sinusoidal load with 70 kg diver
Problem 7
Clamped-clamped model with a sinusoidal load