Description

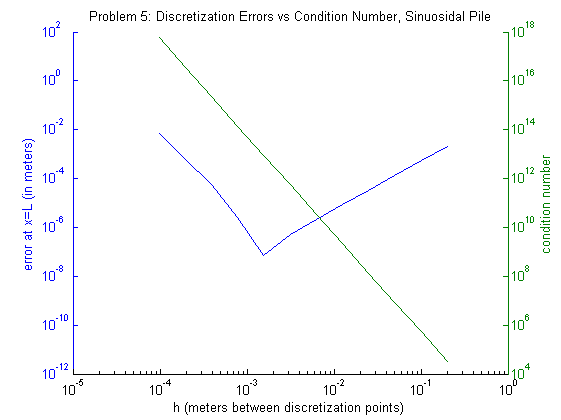
Here we will examine the deflection of our beam with the addition of a sinusoidal load of \( -pg\sin\frac{\pi}{L}x \) where \( p=100kg/m \) and \(g\), \(L\) are as defined on the main page using problem5.m. Our errors at \(x=2m\) are displayed in the following table along with the coresponding condition number of our matrix \(A\).

This table shows that our error decreases until \(n =1280 \), after which it begins to increase again. given our result from Project 3, we think that the relationship might be linear for \(n > 1280\). When \(n \leq 1280\) we would hope the relationship is also linear for consistency. The plot below shows both the condition number (right-green axis) and the error (left-blue axis) for various values of our discretization step \(h\).

Recalling that \(n\) decreases as \(h\) increases, we can see that as \(n\) increases our error follows an inverse linear relationship. This trend shifts sharply at \(n=1280\) where out error begins to exhibit a positive linear relationship. This would suggest that, after \(n=1280\), the condition number begins to have an effect through round-off errors in calculations which prevents us from improving upon the error at \(n=1280\). Our next plot provides a closer look at the relationship between the error and \(h\).

Here we can see that the error is roughly proportional to \(h^2\) as the problem description claims. Further, as stated above, the condition number overpowers any gains from a decrease in \(h\) once \(n>1280\). Next, we will remove this sinusoidal pile and add a 70 kg diver to the final 20 cm of the beam and investigate the deflection in Problem 6.

<< Previous Next >>