|
|
George Mason University
Zakaria Tarik Zerhouni
Source: Home > Project 2 > Step 6 > Conclusion
Math 447: Numerical Analysis
Conclusion:
In Step One and Step Two the Multivariate Newton Method and a closed form solution using the quadratic formula
were employed to check the validity and accuracy of the solutions they output. Both procedures produced nearly identical results
against a provided satellite arrangement and solution with little trouble.
Step Four and Step Five saw the positions selected in order to check the conditioning of the procedures. In this case the
Multivariate Newton's Method was employed.
The three examples addressed showed a significant increase in error magnification factor with more clustered satellite
arrangements.
The well-spaced-out satellites in Step Four had an EMF of 4.3946,
while the moderately clustered satellites in Step Five, Case 1 had an EMF of 71.6852,
and the nearly-touching satellites in Step 5, Case 2 had an EMF of 28,671.
To try to investigate this further, a script was constructed to generate random sets of satellites and compare the angular
distance between them and the EMF of the results they produced. While it is obvious that there are numerous factors involved,
one can see that the EMF is roughly proportionate to the angular distance from Figure 7.1 below.
Figure (7.1)
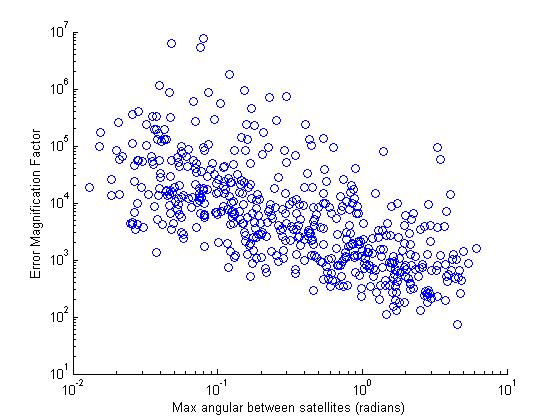
Click on the scatter plot to view the associated code.
Finally, Step Six set out to reduce error by adding more satellites. The most interesting result was that the Gauss Newton
method has no issue with clustered satellites being part of the array so long as adequately spaced out satellites are available.
The EMF is reduced and no loss of precision occurs.
The Gauss Newton method ensures that by using the maximum available satellites
in the GPS system, any clustering issues can be avoided and error can be reduced significantly.
|
