|
|
George Mason UniversityZakaria Tarik ZerhouniThis project was completed in collaboration with Daniel JacobsonWebsite designed by Conor P. NelsonSource: Home > Project 4Math 447: Numerical AnalysisProject 4: The Cooling Fin and the Laplace Equation
For this assignment, we sought to approximate solutions \(u(x,y)\) to partial differential equations of the form
\[ u_{xx} + u_{yy} = f(x,y), \]
also known as Poisson equations, on two-dimensional rectangular domains with various boundary conditions:
Dirichlet boundary conditions, which fix the value of \(u\) on the boundary, Neumann boundary conditions,
which fix the first derivative, and Robin boundary conditions, where the first derivative and value are a
function of one another.
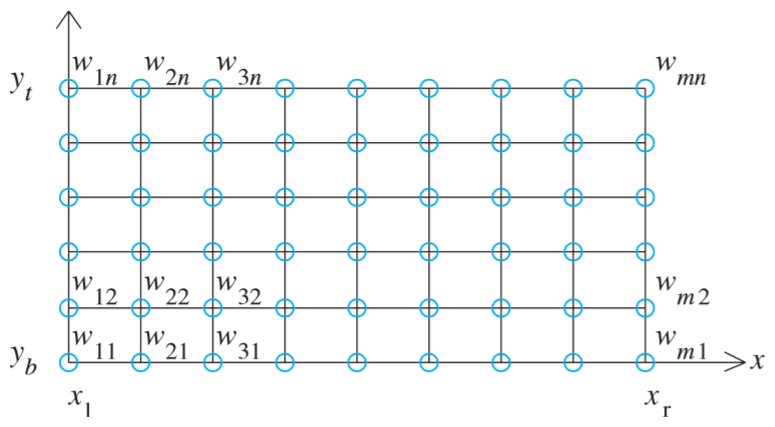
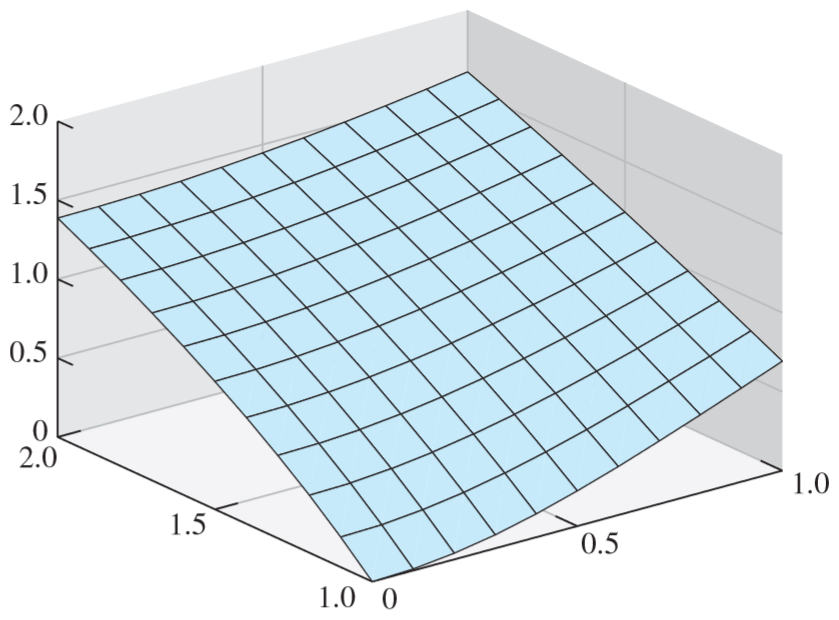
This is done using the Finite Difference Method, discretizing the domain into an \(M \times N\) grid, each
grid square having dimensions \(h \times k\) (see above left), and then constructing a system of linear equations
using the second-order finite difference equation
\[ \frac{w_{i-1,j}-2w_{i,j}+w_{i+1,j}}{h^2} + \frac{w_{i,j-1}-2w_{i,j}+w_{i,j+1}}{k^2} = f(x_i, y_i) \]
for all interior points, and application-specific boundary equations for all others. This system can then be
solved for \(w(x,y) \approx u(x,y)\) on the grid (see above right).
In the following pages we will show two example applications of this method: using Robin boundary conditions
to simulate convection and conduction of heat in a cooling fin, and solving the Laplace equation with discontinuous
Dirichlet boundary conditions.
|