|
|
George Mason UniversityZakaria Tarik ZerhouniSource: Home > Project 2 > Step 2Math 447: Numerical Analysis
Step 2. In order to solve System 1.2 as a closed form solution each component \(x, y, \text{and } z \) were isolated in terms of \(d\). By subtracting the last three equations from the first, three linear equations can be obtained as shown below in System 2.1. System 2.1 \( 2(A_4 - A_1)x + 2(B_4 - B_1)y + 2(C_4 - C_1)z - 2c^2(t_4 - t_1)d - c^2(t_1^2 - t_4^2) + A_1^2 - A_4^2 + B_1^2 - B_4^2 + C_1^2 - C_4^2 = 0 \) \( 2(A_3 - A_1)x + 2(B_3 - B_1)y + 2(C_3 - C_1)z - 2c^2(t_3 - t_1)d - c^2(t_1^2 - t_3^2) + A_1^2 - A_3^2 + B_1^2 - B_3^2 + C_1^2 - C_3^2 = 0 \) \( 2(A_2 - A_1)x + 2(B_2 - B_1)y + 2(C_2 - C_1)z - 2c^2(t_2 - t_1)d - c^2(t_1^2 - t_2^2) + A_1^2 - A_2^2 + B_1^2 - B_2^2 + C_1^2 - C_2^2 = 0 \) Note that System 2.1 can be broken into vectors columns of terms in \(x, y, z, d, \text{and constant terms } w \) by first taking the column vectors of System 2.1 and denoting them as \(x \vec{u}_x, y \vec{u}_y, z \vec{u}_z, d \vec{u}_d, \text{and } \vec{w} \). Thus \(x \vec{u}_x + y \vec{u}_y + z \vec{u}_z + d \vec{u}_d + \vec{w} = \vec{0} \). A formula for \(x\) in terms of \(d\) can be acquired from \( \vec{0} = \) det[\( \vec{u}_y | \vec{u}_z | x \vec{u}_x + y \vec{u}_y + z \vec{u}_z + d \vec{u}_d + \vec{w}\)], \(y\) in terms of \(d\) can be acquired from \( \vec{0} = \) det[\( \vec{u}_x | \vec{u}_z | x \vec{u}_x + y \vec{u}_y + z \vec{u}_z + d \vec{u}_d + \vec{w}\)], \(z\) in terms of \(d\) can be acquired from \( \vec{0} = \) det[\( \vec{u}_x | \vec{u}_y | x \vec{u}_x + y \vec{u}_y + z \vec{u}_z + d \vec{u}_d + \vec{w}\)] Finally by substituting \(x, y, \text{and} z \) in terms of \(d\) back into row one of System 1.2, a quadratic equation in terms of \(d\) is obtained. The quadratic equation, popularly represented as below, is then used to solve for both roots of \(d\). \(r = \frac{-b \: \pm \: \sqrt{b^2 - 4ac}}{2a} \) The results of this method are shown in Figure 2.1 and the associated code can be viewed by clicking on the table. Figure (2.1) 
Click on the table to view the associated code. Figure 2.2 shows the difference in position and time synchronization error for the Multivariate Newton Method and the closed form solution. The differences in position are shown in micrometers to depict just how small they truly are. The difference in time synchronization error is smaller than the precision of the atomic clocks. Figure (2.2) 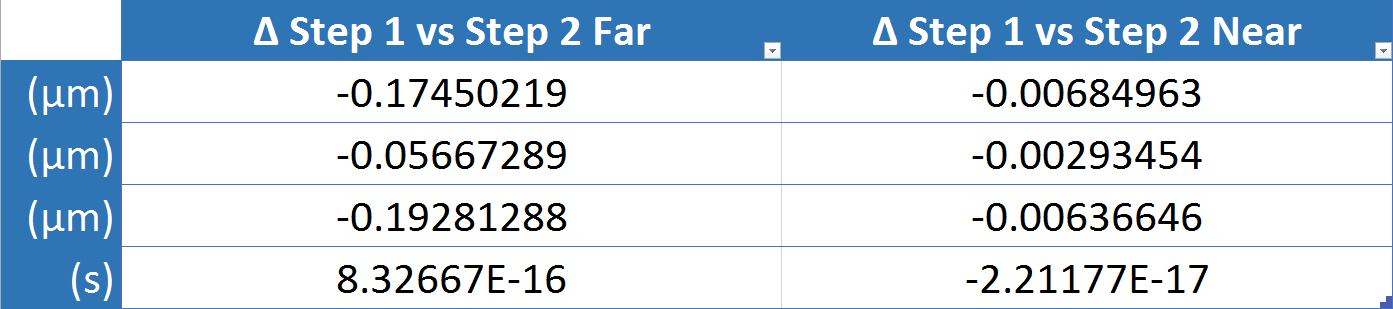
|