|
|
George Mason UniversityZakaria Tarik ZerhouniSource: Home > Project 2 > Step 1Math 447: Numerical Analysis
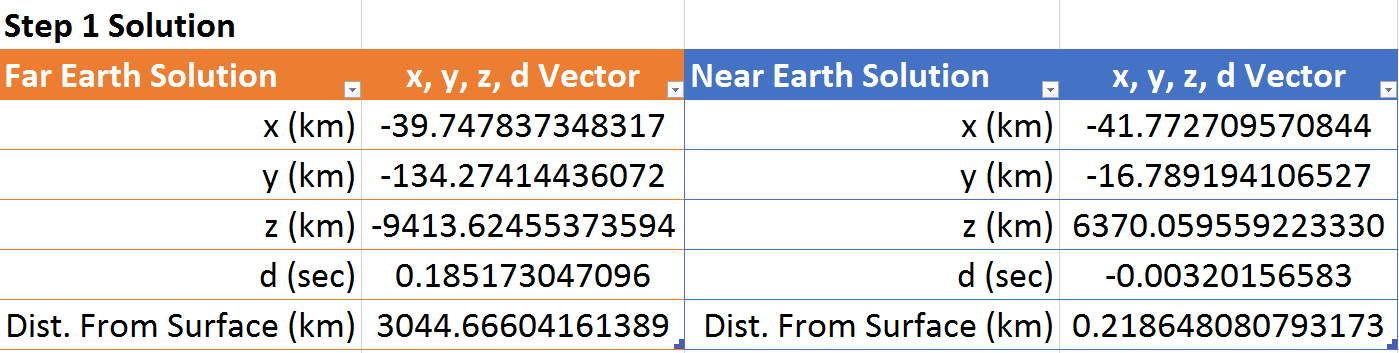
Step 1. For step one, Multivariate Newton's Method was employed to solve for the position and time correction using four satellites. The position solution for \( (x, y, z, d) \) . Using 4 satellites \( (A_i, B_i, C_i, t_i) \) with a known answer, the Multivariate Newton's Method will be tested to solve for the same solution. System 1.1 is algebraically manipulated into the form of System 1.2 below. System 1.2 \( f_1 = (x - A_1)^2 + (y - B_1)^2 + (z - C_1)^2 - (c*(t_1 - d))^2 = 0 \) \( f_2 = (x - A_2)^2 + (y - B_2)^2 + (z - C_2)^2 - (c*(t_2 - d))^2 = 0 \) \( f_3 = (x - A_3)^2 + (y - B_3)^2 + (z - C_3)^2 - (c*(t_3 - d))^2 = 0 \) \( f_4 = (x - A_4)^2 + (y - B_4)^2 + (z - C_4)^2 - (c*(t_4 - d))^2 = 0 \) To solve for \( \alpha = (x, y, z ,d) \) the the Multivariate Newton Method takes the Jacobian matrix of System 1.2 as \( F(\alpha) = (f_1, f_2, f_3, f_4) \) as seen below. \( DF(\alpha) = \left( \begin{array}{ccc} \frac{\delta f_1}{\delta x} & \frac{\delta f_1}{\delta y} & \frac{\delta f_1}{\delta z} & \frac{\delta f_1}{\delta t} \\ \frac{\delta f_2}{\delta x} & \frac{\delta f_2}{\delta y} & \frac{\delta f_2}{\delta z} & \frac{\delta f_2}{\delta t} \\ \frac{\delta f_3}{\delta x} & \frac{\delta f_3}{\delta y} & \frac{\delta f_3}{\delta z} & \frac{\delta f_3}{\delta t} \\ \frac{\delta f_4}{\delta x} & \frac{\delta f_4}{\delta y} & \frac{\delta f_4}{\delta z} & \frac{\delta f_4}{\delta t} \end{array} \right) \) This Jacobian matrix is \( DF(\alpha) = \left( \begin{array}{ccc} 2(x - A_1) & 2(y - B_1) & 2(z - C_1) & 2c^2(t_1 - d) \\ 2(x - A_2) & 2(y - B_2) & 2(z - C_2) & 2c^2(t_2 - d) \\ 2(x - A_3) & 2(y - B_3) & 2(z - C_3) & 2c^2(t_3 - d) \\ 2(x - A_4) & 2(y - B_4) & 2(z - C_4) & 2c^2(t_4 - d) \end{array} \right) \) Beginning with an initial vector \(\alpha_0 \) we iterate through \(n \in \Bbb N \) steps of the process of solving \( \left\{ \begin{array}{lr} DF(\alpha_k)s = -F(\alpha_k) \\ \alpha_{k+1} = \alpha_k + s \end{array} \right.\) for \( k = 0, 1, \ldots , n \).
Depending on the initial vector \( \alpha_0 \) two solutions are computed this way.
|