George Mason University

Zakaria Tarik Zerhouni

Step 6.
The goal of step six is to discover if the GPS error and condition number can be reduced by increasing the number of satellites used to compute the position and time synchronization error.

As there are four variables being solved for as \( (x, y, z, d) \), the addition of one or more satellites will not allow our matrix to be square any longer. In order to handle this the Gauss-Newton Method is employed.

We will briefly describe the process of the Gauss-Newton method. If \(n\) satellites are employed for the solution, with \(n \geq 4\) then a matrix in \(n \times 4\) is produced.

This matrix,

\(r_1(x, y, z, d) \)
\(r_2(x, y, z, d) \)
\(r_3(x, y, z, d) \)
\(\vdots\)
\(r_n(x, y, z, d) \)

will then have its Jacobian taken as \( A = Dr(x, y, z, d) \).

Denote \(\alpha_0 = ( x_0, y_0, z_0, d_0 ) \). We converge to a solution by iterating through \(m \in \Bbb N \) steps of solving

\( \left\{ \begin{array}{lr} A^TAv_k = -A^Tr(\alpha_k) \\ \alpha_{k+1} = \alpha_k + v \end{array} \right.\)

for \( k = 0, 1, \ldots , m \).

For an initial vector \( \alpha_0 = (0, 0, 6370, 0) \) was utilized. Figure 6.1 below displays the condition number of each matrix \(A^TA\) and the position error calculated as \( \sqrt{x_{err}^2 + y_{err}^2 + z_{err}^2} \).

Figure (6.1)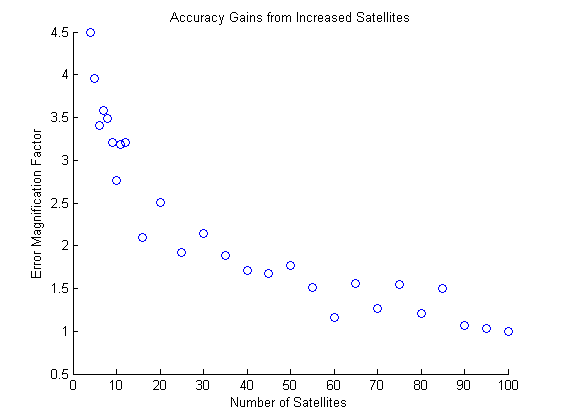

Click on teh image to view the associated code.



Figure (6.1)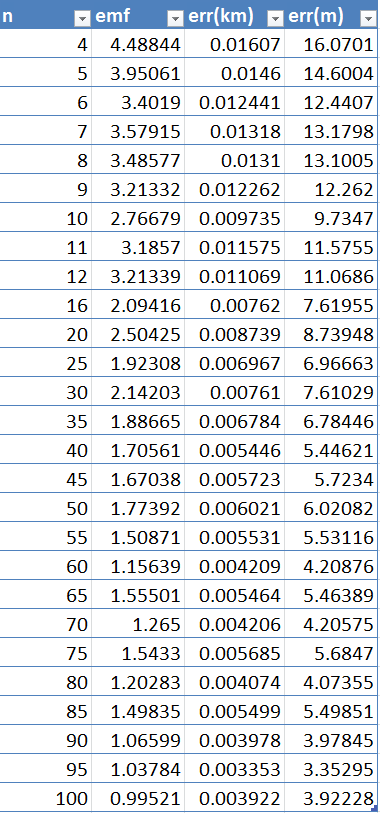

Click on the table to view the associated code.

Figure 6.1 shows that increasing satellites reduces the EMF and provides a reduction in error. While the number of satellites required for increased precision is high, there is a benefit associated with them in the Gauss-Newton Method.

Previous: Step 5

Project 2 Home

Next: Conclusion