George Mason University

Zakaria Tarik Zerhouni

Step 5.
In Step 4 we chose widely spaced satellite coordinates and got a condition number of 4.3946.
We will now proceed to alter the spacing of the satellites in order to check the error and condition number under the new conditions.

Case 1: When the satellites are somewhat clustered.

This is done first without error, and then with 10 nanoseconds of error:

>> part4(0, [0.5, 0.75, 1.0, 1.25], [1.5, 2.0, 2.5, 3.0])
maxerr =
3.2742e-11
ans =
Inf

>> part4(10^-8, [0.5, 0.75, 1.0, 1.25], [1.5, 2.0, 2.5, 3.0])
maxerr =
0.2149
ans =
71.6852

Below is the generated 3D plot of Case 1, Figure 5.1.

Figure (5.1)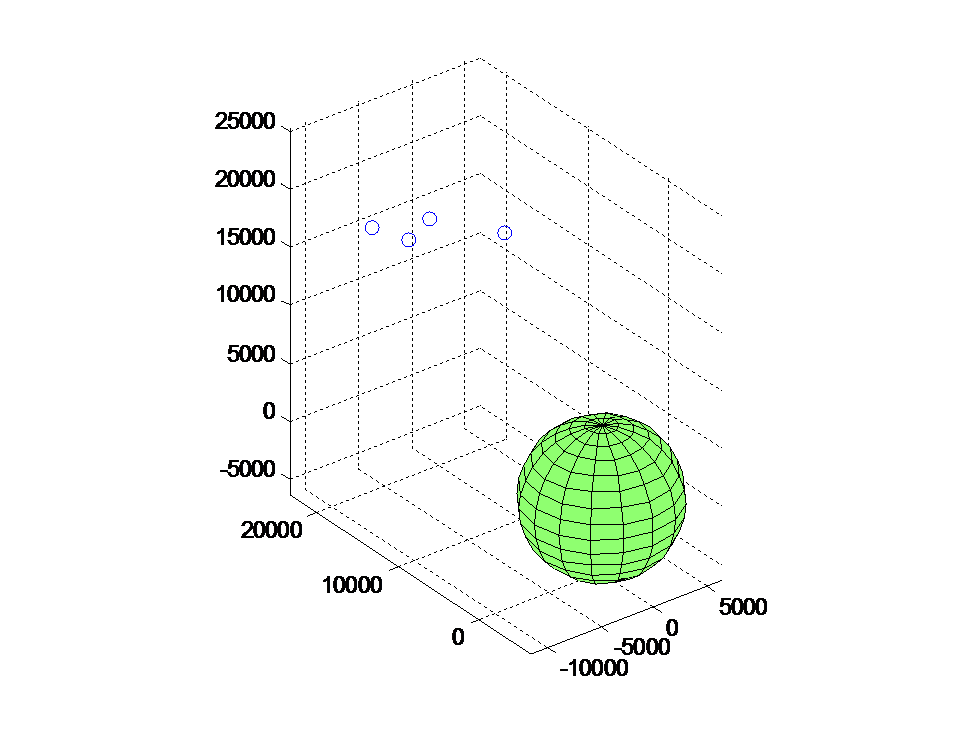

Click on the image to view the associated code.

As shown by the first function call (with no input error), the equation is still solvable at machine precision (with an output error in the nanometers), the error magnification factor is much higher than before; a timing error of 10 nanoseconds results in an error of 215 meters in the calculated position.

Case 2: When the satellites are tightly clustered.

Once again, the code is run first without error, then with 10 nanoseconds of error:

>> part4(0, [0.70, 0.71, 0.72, 0.73], [2.15, 2.1, 2.05, 2.0])
maxerr =
1.0927e-07
ans =
Inf

>> part4(10^-8, [0.70, 0.71, 0.72, 0.73], [2.15, 2.1, 2.05, 2.0])
maxerr =
859.5457
ans =
2.8671e+05

Below is the generated 3D plot of Case 2, Figure 5.2.

Figure (5.2)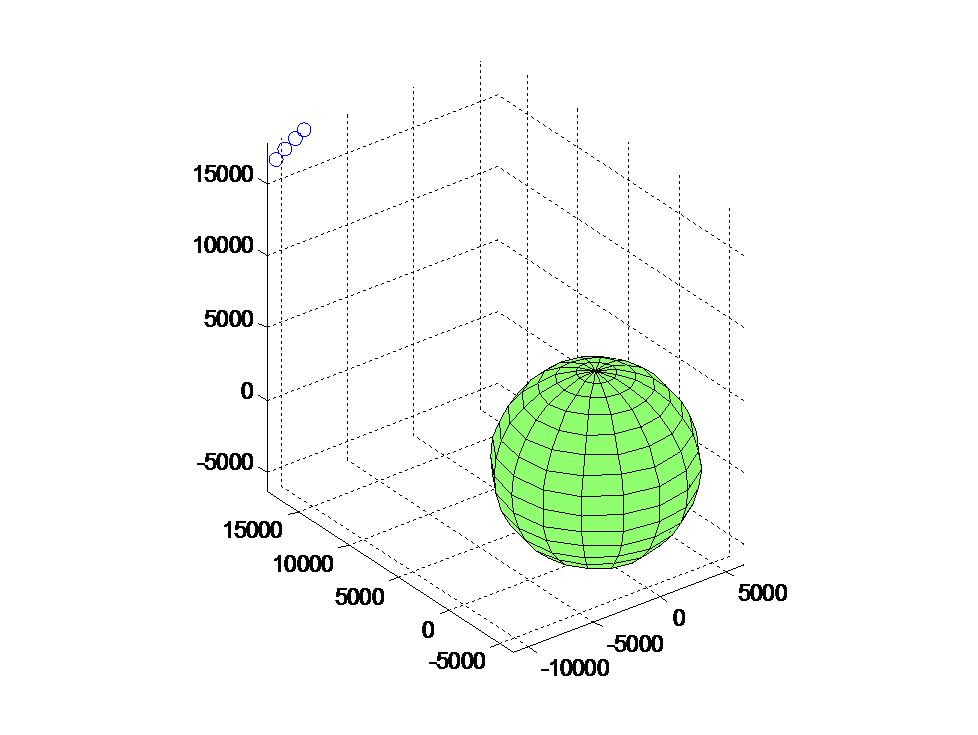

Click on the imge to view the associated code. This code is the same as in Figure 5.1.

As we can see, closer groups of satellites have much higher error magnification. The calculation at machine precision gets somewhat less precise (with error on the order of micrometers), but the introduction of a 10 nanoseconds of timing error results in a massive output error of 859km.

A Special Case: When the satellites are all at an identical inclination

When \(\phi\) is the same for all four satellites, the method reports a singular matrix and fails completely, despite the satellites being spaced equally far apart:

>> part4(10^-8, [0.5, 0.5, 0.5, 0.5], [0, pi/2, pi, 1.5*pi])

Below is the generated 3D plot of the Special Case, Figure 5.3.

Figure (5.3)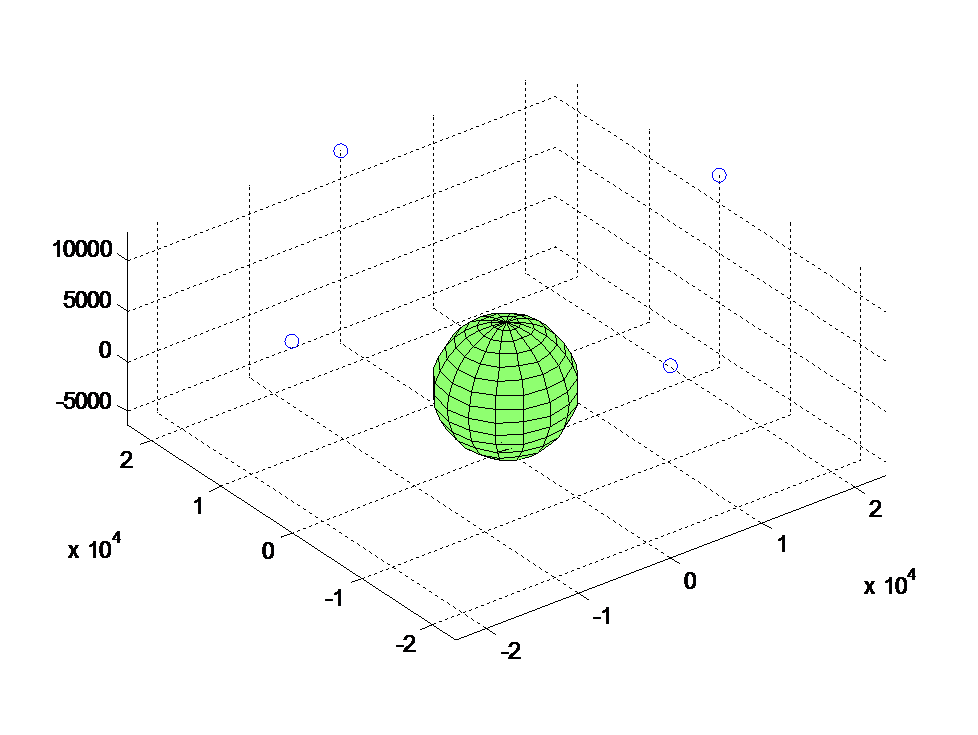

Click on the image to view the associated code. This code is the same as in Figure 5.1.

Interestingly enough, this does not occur when the value of \(\theta\) is held constant. We determined that this is because the observer is at the north pole. Thus if all four satellites are at the same latitude, they are equidistant from the observer and depending on the value of d could place the observer at any point along the z-axis.

Previous: Step 4

Project 2 Home

Next: Step 6