Problem 1: We setup Matlab code using Adaptive Quadriture to determine the length of a segment of a parametrized curve. The curve is parametrized as t from 0 to T, and the function can return the length of the arc when t is set to any value from 0 to T. The equations for x and y are:

• x(t) = 0.5 + 0.3t + 3.9t^2 - 4.7t^3
• y(t) = 1.5 + 0.3t + 0.9t^2 - 2.7t^3
• x'(t) = 0.3 + 7.8*t - 14.1*t^2
• y'(t) = 0.3 + 1.8*t - 8.1*t^2

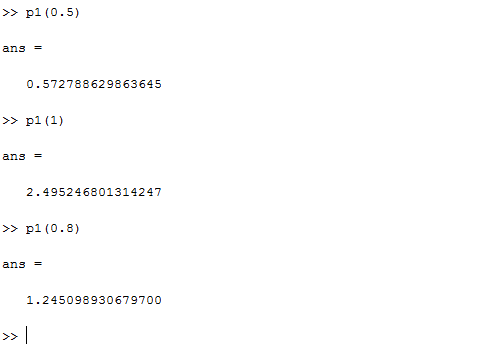
The total length (t=1) was determined to be 2.49. The halfway point for t (t=0.5) gives an arc length of just 0.57, and t=8 gives 1.25. This shows that t and the length do not increase at the same rate. The majority of the length of the arc is found when t is above 0.5. Here's the Matlab code for adaptive quadriture, and here's the code that calls it.

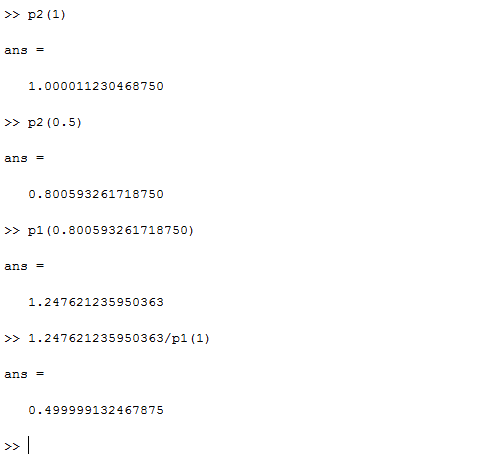
Problem 2: We developed code in order to be able to specify a parameter s representing a fraction of the total arc length, and compute the t parameter value which would result in that particular length value along the arc. The function being set to 0 is adapquad(f_arc, 0, t, 0.5e-6)/adapquad(f_arc, 0, 1, 0.5e-6) - s. The solution is found using the bisection method, with the starting interval (-0.5e-3 to 1 + 0.5e-3). The code used to solve this problem can be found here. The bisect method code called in the solution is visible here.

Problem 3: We created Matlab code to split the arc into equal length components. For example, if n = 5, then the arc will be separated into 5 pieces of equal length, and their t parameter values will be given. In the example to the right, the t value (0.935) that is 4/5 of the way along the curve is plugged back in to demonstrate that t = 0.935 is required to get to that point. Here's the code.

Problem 4: We repeated parts 2 and 3 with newton's method in place of the bisection method. The speed increase was not very impressive, but it does appear to be somewhat faster than using bisection. In the example to the right, the Newton's approach took 4.05 seconds, and the bisect one was 6.26, so 4.05/6.26 = 0.65. The Newton's code takes about 65% of the time to execute as the bisect based implementation. The driving code can be seen here, and here is the newton's method Matlab file. Code for the test: here.

Problem 5 (Even arc length): Movies of a particle moving around the arc were created. One version contains increments of the parameter t that are constant, and the other keeps the arc length increments constant. This demonstrates the relationship between s (length) and t. Files used for this problem:

• MakeQTMovie
• animate
• npartition
• ntstar
• arclength

Problem 5 (Even t parameter length): Here's the case in which the t parameter was incremented at constant intervals. This caused the arc length to vary at different rates throughout the trip.

Problem 7: In the case of problem 7, a progress curve C(s) was used to further control the rate of advancement of the point along the curve. C(s) = s would represent constant speed, C(0) = 0, and C(1) = 1. If the polynomial C(s) = 4*s^3 - 6*s^2 + 3*s is used, the point comes to a stop in the middle of the arc, after which it begins accelerating again on the other side. Additional Matlab files used for this problem:

• animate (Modified for C(s))
• npartition (Modified for C(s))