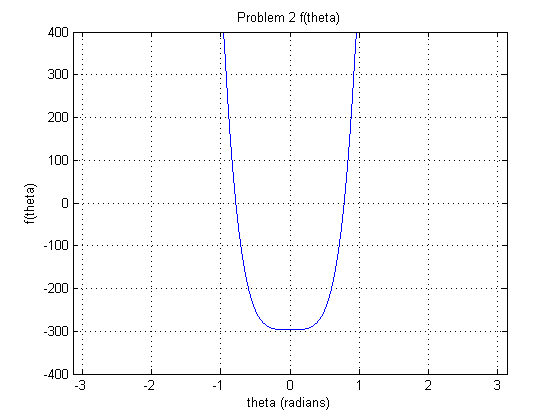
Problems 1 and 2: We set L1 = 2, L2 = L3 = sqrt(2), gamma = pi/2, and p1 = p2 = p3 = sqrt(5), x1 = 4, x2 = 0, y2 = 4. We created a Matlab function f(theta), available here, which takes an angle as input, and the constants listed above hard coded within it, and returns a single value. A root represents a pose for the platform. We found the roots of a configuration of the Stewart Platform graphically, as well as using the bisect method code taken directly from the text, here. The bisect method was able to find the negative pi/4 root with the starting interval (-0.8, -0.6), and the positive pi/4 root with (0.6, 0.8) because f(theta) was positive on one side and negative on the other for both of these intervals, and the intermediate value theorem says that there is a root somewhere in the interval in that case. The advantage of the Bisection method is that it doesn't requre manipulation or differentiation of complicated equations in order to find a root, which is why it was used instead of fpi or Newton's method.

Problem 3: Graphs matching those in figure 1.15 in the textbook were created using Matlab's plot function. This exercise was practice for creating similar figures for the remaining problems. The strut lengths can be measured using the Pythagorean Theorem to check that they match the given values of p1, p2, and p3 for the given problem. The code used to create all of the figures in this presentation is here.

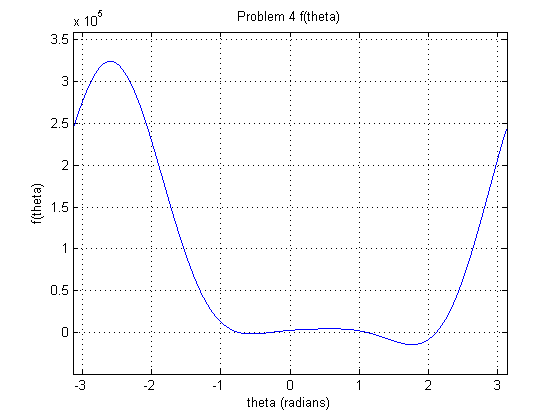
Problem 4: We set x1 = 5, x2 = 0, y2 = 6, L1 = 3, L2 = 3*sqrt(2), L3 = 3, gamma = pi/4, p1 = 5, p2 = 5, p3 = 3. We created a new version of the Matlab file with the new starting values, which can be viewed here. We found four roots using both graphing and the bisect method for verification. We also created graphs of the four poses corresponding to the four roots similar to the ones in figure 1.15, which were graphed as a test in the previous problem. Using the Pythagorean Theorem, we verified that p1, p2, and p3 matched the strut lengths in the four graphs of the poses. The four roots were located at theta = (-0.720849037170410, -0.331006050109863, 1.143685340881348, 2.115908622741699).

Problem 5: All of the starting values from problem 4 except p2 were left alone for this problem. The modified version of the Matlab function is available here. We found 6 roots when p2 was changed to 6.985, which is very close to 7 (the original working value of p2 given, which was confirmed to give 6 roots). We found this value by changing p2 in small amounts, and plotting the function from -pi to pi each time to check the number of roots. It was necessary to create a graph with the y-axis scale reduced in order to be able to see all 6 roots clearly. This is because in the area from -1 to 1, it's not easy to see how many times the function crosses the x-axis without zooming in on that part of the function. After finding the roots graphically, the result was also checked using the bisection method as well. Afterwards, figure plots of the poses were created using Matlab's plot command. The roots we found were (-0.7070498898799997, -0.2771350100229030, -0.0004772047803271561, 0.4546179375087377, 0.9780956462163883, 2.512221400131239).

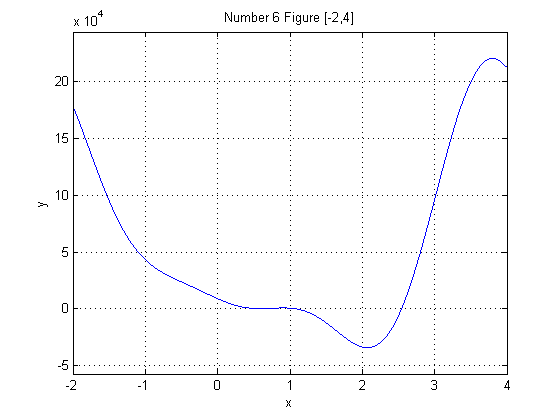
Problem 6: This exercise was based on the same starting values as problem 4, except for p2. We varied p2 in integer amounts in order to find a configuration of the Stewart Platform with only two roots/poses. We found that for p2 = 8, there are only 2 roots. The altered version of the Matlab function is available for viewing here. Figure graphs were also created for these poses. The roots were (1.07091899840162, 2.544259100127965).