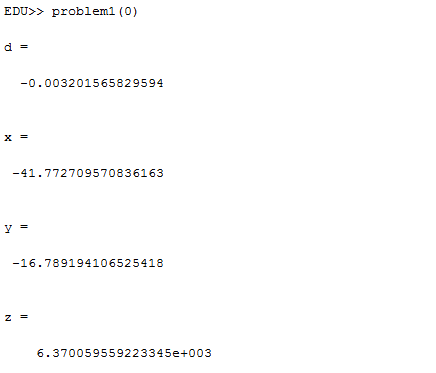
Problem 1: We needed to calculate the position of the receiver based on information from four satellites. We solved four equations in four unknowns by subtracting the second, third, and fourth from the first, and then using determinants to get equations for x, y, and z in terms of d. Once we had these equations, we substituted them all into the first equation in order to get an equation with only d. After consolidating constants, we used the quadratic formula to find the two solutions. The Matlab code used can be seen here. The first solution for the location of the observer is (x, y, z, d) = (-41.772709570836163 km, -16.789194106525418 km, 6370.059559223345 km, -0.003201565829594 s). This location puts the observer on the surface of the Earth. We also found the second, away from Earth solution: (x, y, z, d) = (-39.747837348212244 km, -134.2741443606902 km, -9413.624553735819e km, 0.185173047095946 s).

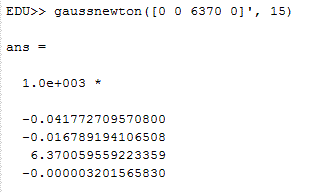
Problem 3: We solved the same problem for the two solutions as problem 1, but using the multivariate Newton's Method rather than the algebraic approach. We achieved this by creating a Jacobian Matrix for the equations by taking the partial derivative with respect to each variable x, y, z, d, and making those the elements of one row of the matrix. Each equation was turned into a row in the Jacobian Matrix through this process. Then, we applied Gauss-Newton multivariate iteration to solve the system. The first solution is: (x, y, z, d) = (-41.772709570800 km, -16.789194106508 km, 6370.059559223359 km, -0.003201565830 s). This was found with the starting vector [0 0 6370 0], and is the same as the on Earth solution found in problem 1. The other solution can be found by providing a starting vector with a large initial guess for d, such as [0 0 6370 1]. For the far from Earth solution, we found (x, y, z, d) = (-39.747837348626 km, -134.274144360851 km, -9413.624553736307 km, 0.185173047096 s). Both of these solutions are the same as the two solutions found using the algebraic determinant method in problem 1. The Matlab code used can be read here.

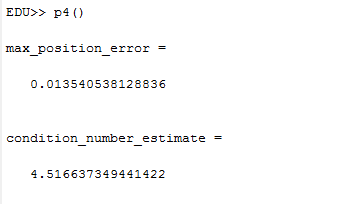
Problem 4: We looked at the error associated with small changes to the travel times for signals from four unbunched satellites. We first found the solution for a system of four satellites, and then solved the system with error in the travel times for the signals. The error in the travel times was either 10^(-8), or -10^(-8), and these errors were added to the travel times for the four satellites. This error caused a change in the position values we found for the receiver. There were 14 possible ways of adding the two values for time errors (10^(-8), -10^(-8)) for the four satellites (the problem stated that all the errors added to the travel times shouldn't be the same, so it's 14 instead of 2^4 = 16), which we iterated through in order to find the maximum position error and maximum Error Magnification Factor. The Error Magnification Factor was defined as the maximum position error for a particular iteration divided by the speed of light times the travel time error. The maximum EMF for all the combinations was the estimate for the condition number, which was 4.516637349441422. The maximum position error for all of the 14 iterations that we tried was 13.540538128836 meters. The code used to solve this problem is broken into two parts: the modified gauss_newton file, and the overall p4 file, which runs the entire process.

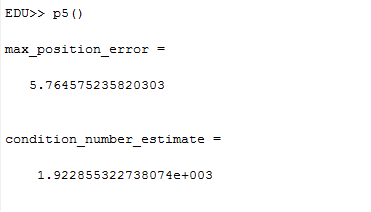
Problem 5: We ran the same exact process as for problem 4, except with satellites that were all bunched together in the sky. In this case, the spherical coordinate theta and phi values for the satellite positions were all within 5% of one another. In this configuration, we found that the maximum position error and Error Magnification Factor went up dramatically to very high values, indicating that bunched up satellites don't work very well for determining the position of a receiver. The maximum EMF, or condition number we found was 1922.855322738074, and the maximum position error was 5764.575235820303 meters. The matlab code used can be found here (newton) and here (p5 general).

Problem 6: We added 5 additional satellites to the configuration from problem 4, with the nine satellites unbunched, and distributed across the sky. We tried different combinations of the possible (10^(-8), -10^(-8)) errors added to the satellite signal travel times. We found the condition number (max EMF) 2.447353140159228, and the maximum position error, 7.336980134824 meters. Out of the three configurations we explored, (four spread out, four bunched together, nine spread out), we found that the best one was 9 satellites spaced out. This gave the lowest condition number of 2.45, and the lowest GPS position error of 7.34 meters. The error was very high for the four bunched case, and the 4 unbunched case was about half as accurate as the 9 unbunched case. The code used for problem 6 is available here (newton) and here (overall p6).