|
|
George Mason UniversityZakaria Tarik ZerhouniSource: Home > Project 3 > Step 5Math 447: Numerical Analysis
Computer Problem 6.3.8 aims to create a system of differential equations to model a double pendulum, where a second rod and bob hang from the first bob of the original pendulum model. In order to accomplish this we used simple trigonometry to solve for the position of the second bob and animated the second rod from the first bob to the second bob. Figure 5.1 below is a simple graphic detailing this procedure. Figure 5.1 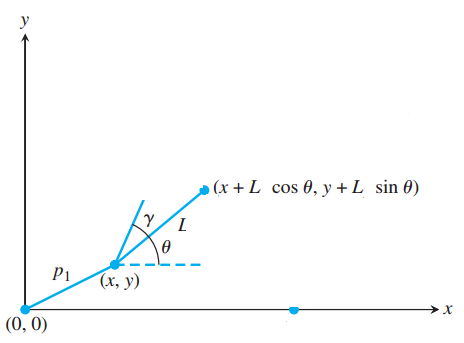
Below is the system of differential equations provided to model the double pendulum where \(y_{rod1} \) is the angular position of the first pendulum and \(y_{rod2} \) is the angular position of the second pendulum (still relative to the vertical axis). To describe the system of the equations we set \( y_{rod1} = y_1, y_{rod1}' = y_2, y_{rod2} = y_3, \text{and } y_{rod2}' = y_4 \). \(y_1' = y_2\) \(y_2' = \frac{( (-3 g y_1 - g \sin(y_1 - 2 y_3) - 2 \sin(y_1 - y_3) (y_4^2 + y_2^2 \cos(y_1 - y_3)))}{(3 - \cos(2 y_1 - 2 y_3 )) ) } - dy_2 \) \(y_3' = y_4\) \(y_4' = \frac{( 2 \sin(y_1 - y_3) (2y_2^2 + 2g\cos(y_1) + y_4^2\cos(y_1 - y_3)) )}{(3 - cos(2 y_1 - 2 y_3))}\) We show below two cases of stable periodic motion of the downward position and finally a case of sustained non-periodicity. IC = [0.1, 0, 0, 0]Click here to see the code used to generate these animations. Click here to download the video. IC = [\(\frac{\pi}{2}\), 0, \(\frac{\pi}{2}\), 0]Click here to see the code used to generate these animations. Click here to download the video. IC = [\(\pi\), 0, \(\pi\), 0]Click here to see the code used to generate these animations. Click here to download the video.
|