George Mason University

Zakaria Tarik Zerhouni

Multiple attractors and chaotic motion.

Computer problem 6.3.5 uses the same simulation of a force, damped pendulum but changes the forcing parameter \( A \). It contains two "attracting" solutions that periodically change directions at four angles between \(\theta = 0\) and \(\theta = 2 \pi \).

The videos of the solutions below animate this behavior and Table 2.1 shows the approximate locations of direction changes at twenty-four sampled angles. The positions highlighted in blue represent Solution 1 and the positions highlighted in red represent Solution 2.

Solution 1

Click here to see the code used to generate these animations.
Click here to download the video.

Solution 2

Click here to see the code used to generate these animations.
Click here to download the video.

Table 2.1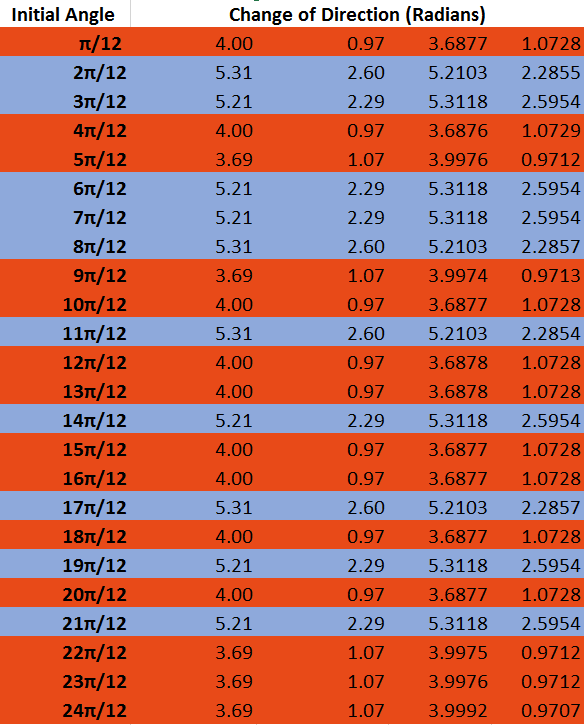


Click on the table to view the associated code.

Table 2.2 addresses checks twenty-four positions of the pendulum at the initial conditions of \( ( y_1, y_2 ) = ( \text{angular position}, \text{velocity} ) \) for \( (y_1, y_2) = \{ (a, 0), (b, 0) \} \), where \( |a -b| \leq 0.1 \).

Our goal in checking these positions is to see if within this difference of angular position a different soultion is achieved.

Table 2.2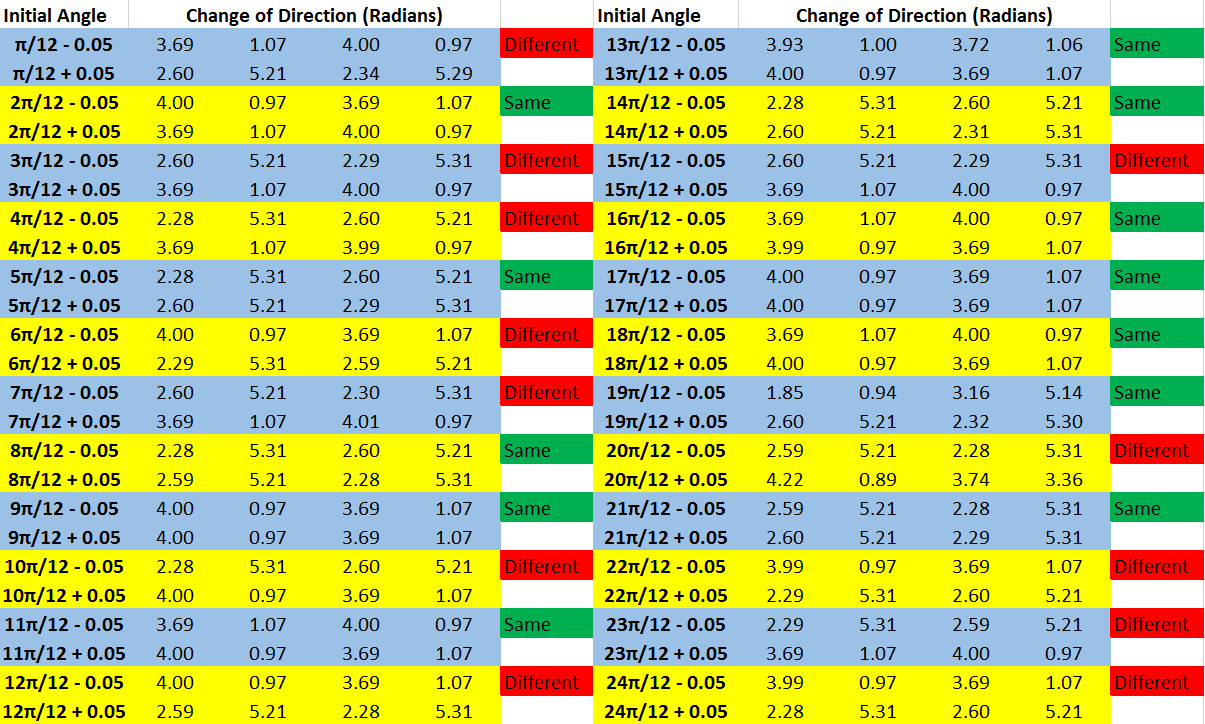


Click on the table to view the associated code.

Finally, below is a video of the forced damped pendulum with a forcing parameter of \( A = 15 \). This parameter causes chaotic motion.

Chaotic Motion

Click here to see the code used to generate these animations.
Click here to download the video.

Previous: Step 1

Next: Step 3