Introduction

In the following problems, we apply the 2-dimensional discrete cosine transform, defined by the matrix in dctMat.m, using twoDimDCT.m. This is inverted using invertTwoDimDCT.m which is simple due to the orthogonal nature of the matrix. Since we are attempting to work with a non-square image, we have the function tosquare.m to make the image data into a square matrix and then we take the relevant data from the resultant square matrix to reconstruct the original image which is 2448 x 3264 which may be found here.

Part 1 - Computer Problem 11.2.3

Using problem3.m, we may obtain the following figures of an 8x8 block with various linear quantization loss parameters. We started with a color image and converted to grayscale using rgbim2gray.m. Upper left corner is (1,96) from the original image. Left image is the base 8x8 block. Right images have loss parameters \(p=1,\,2,\,4\).

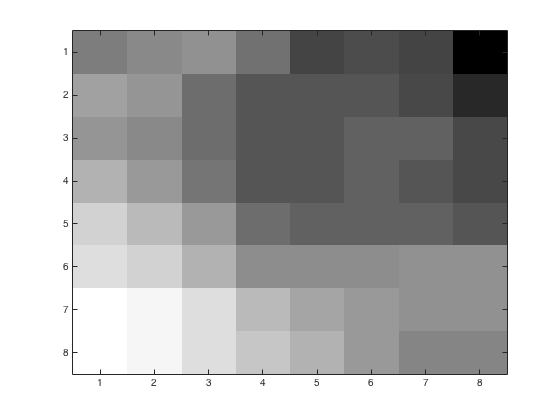
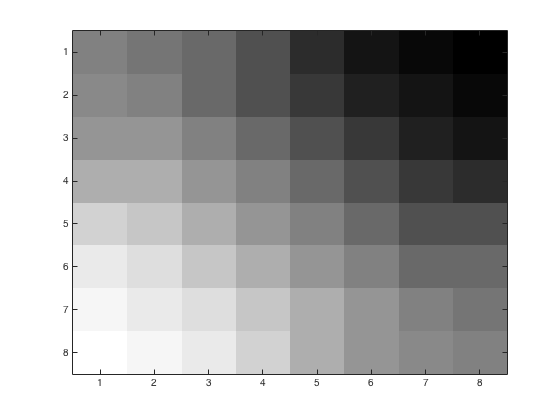
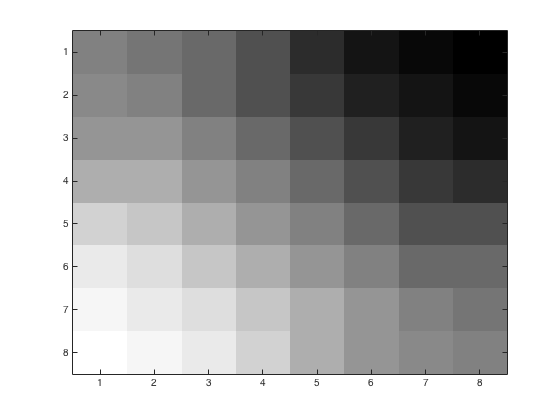
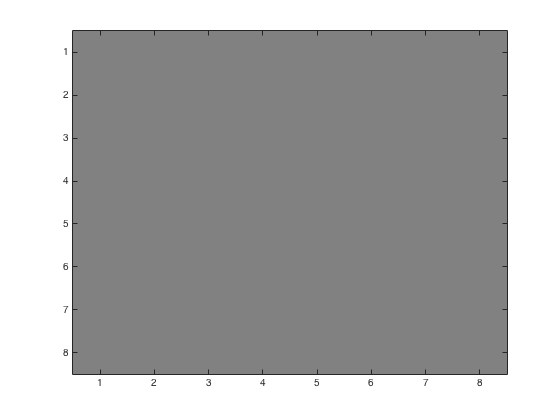
The \(Y_Q\) matrices for each of the 8x8 blocks, while unsightly are as follows:

\(p=1:\begin{pmatrix} 41 & 2 & 0 & 0 & 0 & 0 & 0 & 0\\ -2 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0& 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0& 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} \) \(p=2:\begin{pmatrix} 21 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\ -1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} \) \(p=4:\begin{pmatrix} 10 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ \end{pmatrix} \)

The reconstituted image with loss parameters \(p=1,\,2,\,4,\,14\) (14 for the sake of seeing some effect). All following reconstituted images created by compressimquant.m

Part 2 - Computer Problem 11.2.4

Using problem4.m, we may obtain the following figures of an 8x8 block with various JPEG quantization loss parameters. We started with a color image and converted to grayscale using rgbim2gray.m. Upper left corner is (1,96) from the original image. Left image is the base 8x8 block. Right images have loss parameters \(p=1,\,2,\,4\)

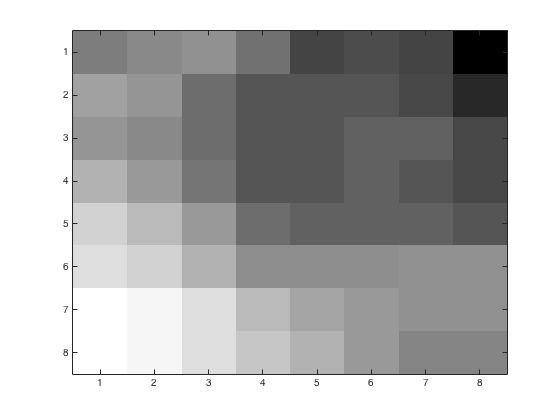
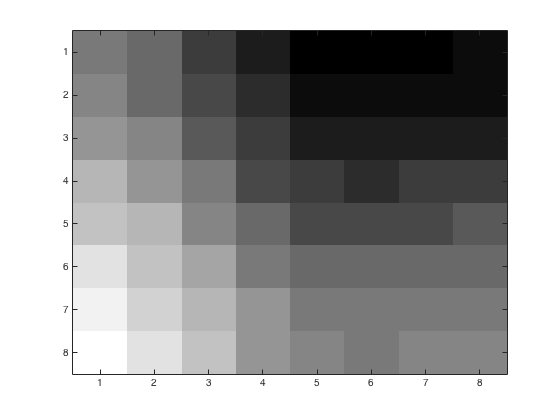
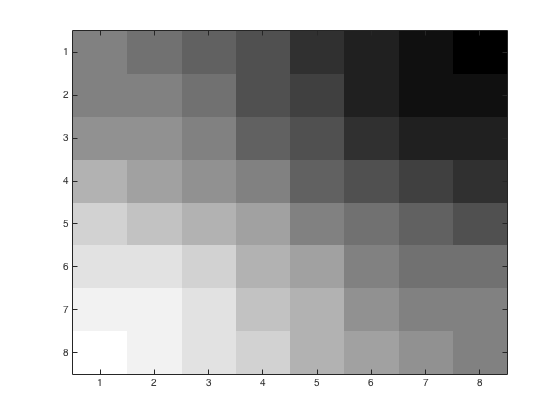
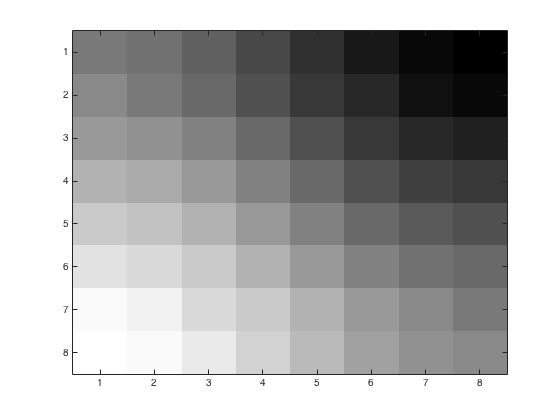
The reconstituted image with loss parameters \(p=1,\,2,\,4\)

Part 3 - Computer Problem 11.2.5

Using problem5.m, we may obtain the following figures of an 8x8 block with various linear quantization loss parameters. This time we stay with the RGB color system throughout the process. Upper left corner is (482,1900) from the original image. Left image is the base 8x8 block. Right images have loss parameters \(p=1,\,2,\,4\)

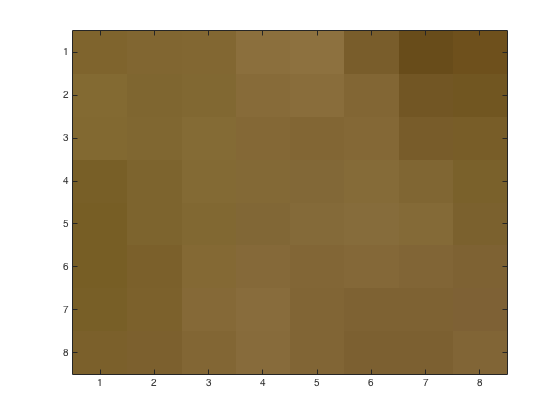
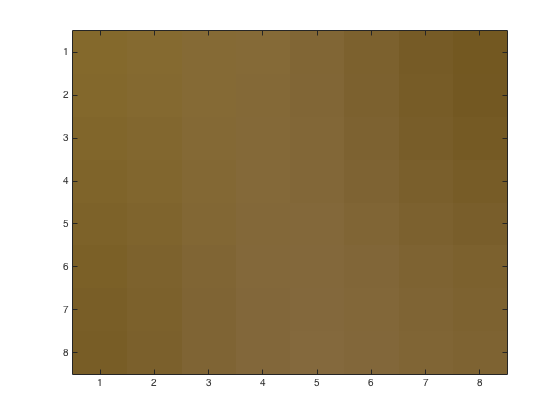
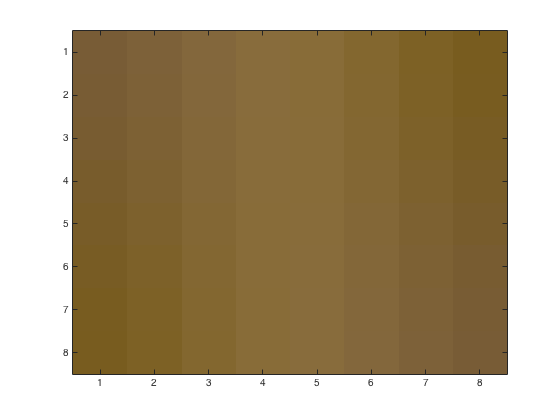
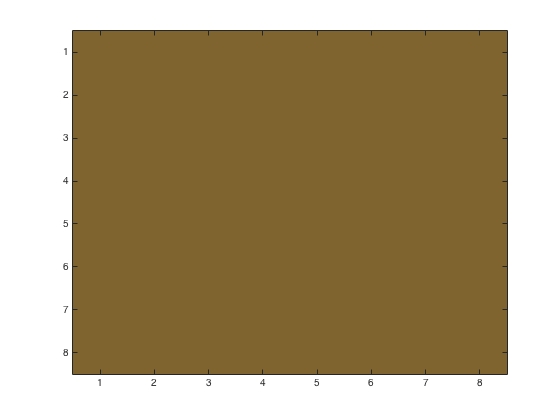
The reconstituted image with loss parameters \(p=1,\,2,\,4\)

Part 4 - Computer Problem 11.2.6

Using problem6.m, we may obtain the following figures of an 8x8 block with various JPEG quantization loss parameters. This time we initially convert from RGB to luminance with rgbim2luminance.m and at the end back to RGB with lum2rgb.m. Upper left corner is (482,1900) from the original image. Left image is base 8x8 block. Right images have loss parameters \(p=1,\,2,\,4\)

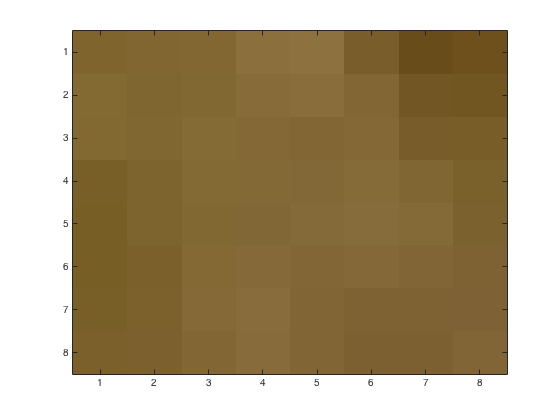
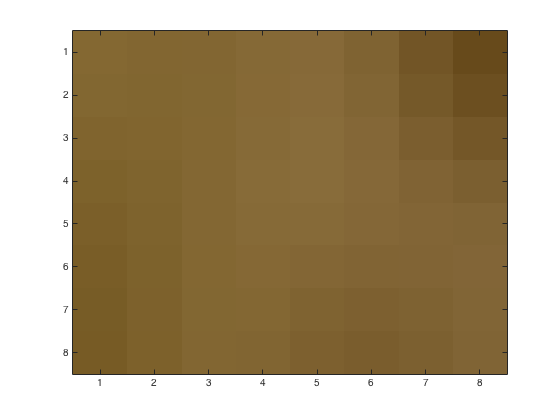
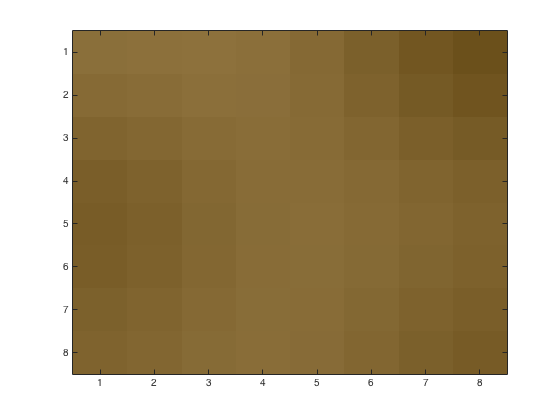
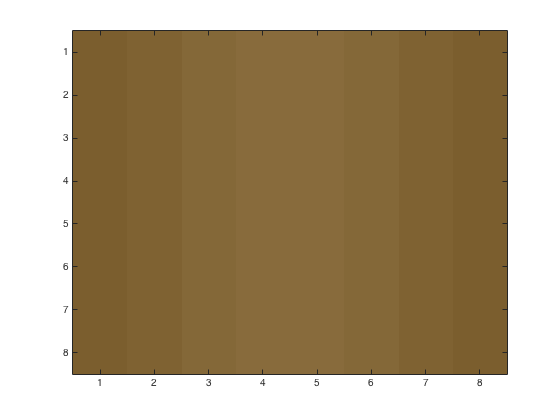
The reconstituted image with loss parameters \(p=1,\,2,\,4\)