By: Roque Donoso, Conor Nelson, Peter Rizzi
This problem can be found on pages 238-241 of Numerical Analysis by Timothy Sauer.
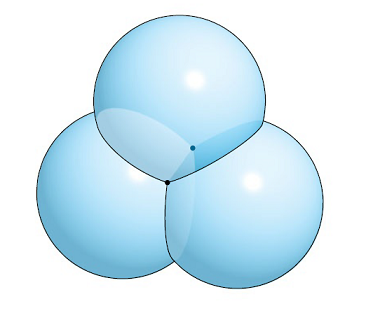
The main purpose of this assignment is to try and delve into the mechanics of the Global Position System (GPS) and thus try to get a basic understanding of how it functions. GPS consists of 24 satellites orbiting the earth at any given time; there being five to eight satellites in the direct line of sight from any point on Earth. The main objective of each satellite is to transmit signals from predetermined positions in space so that these signals are picked up by receivers. The receivers are then able to use the signals to determine their position. This process works by looking at the spherical ranges of the three satellites, and proceeding to calculate the intersection point between the three spheres, as seen on Figure 1.
However, although the satellites use atomic clocks and are thus fairly accurate, the receivers on Earth donít have atomic clocks and so have poor accuracy. This results in the addition of a fourth satellite in order to fix the inaccuracy in the receiver. We are then left with four equations to solve for 4 unkowns; x, y, z, d. Solving the system results in knowing the location of the receive, as well as the correct time from the satellite clocks.
Step 1
We solved the following system using Multivariable Newtons Method:
\[ \begin{align} r_1 (x,y,z,d) = \sqrt[2]{(x-A_1)^2 + (y- B_1)^2 + (z- C_1)^2}-c(t_1 -d) = 0 \\ r_2 (x,y,z,d) = \sqrt[2]{(x-A_2)^2 + (y- B_2)^2 + (z- C_2)^2}-c(t_2 -d) = 0 \\ r_3 (x,y,z,d) = \sqrt[2]{(x-A_3)^2 + (y- B_3)^2 + (z- C_3)^2}-c(t_3 -d) = 0 \\ r_4 (x,y,z,d) = \sqrt[2]{(x-A_4)^2 + (y- B_4)^2 + (z- C_4)^2}-c(t_4 -d) = 0 \end{align} \]
The satellites are given with the following positions in km: \((15600,7540,20140)\), \((18760,2750,18610)\), \((17610,14630,13480)\), \((19170,610,18390)\). The measured time intervals, respectivly, in seconds are: \(0.07074,0.07220,0.07690,0.07242\). We set our intial vector to be \((x_0, y_0, z_0) = (0,0,6370,0)\). Running our code then results in the following solution.
Step 2
We are now asked to algebraically solve our system by using the quadratic formula. We can rewrite our equations in the following way:
\[ \begin{align} \\(x-A_1)^2 + (y- B_1)^2 + (z- C_1)^2 = c(t_1 -d)^2 \\ \\(x-A_2)^2 + (y- B_2)^2 + (z- C_2)^2 = c(t_2 -d)^2 \\ \\(x-A_3)^2 + (y- B_3)^2 + (z- C_3)^2 = c(t_3 -d)^2 \\ \\(x-A_4)^2 + (y- B_4)^2 + (z- C_4)^2 = c(t_4 -d)^2 \end{align} \]
Subtracting the last three equations from the first equation results in three linear equations in the four unknowns:
\[ \begin{align} \\x*Ux + y*Uy + z*Uz + d*Ud + W = 0\\ \end{align} \]
A formula for x in terms of d can be obtained from: \[ \begin{align} \\0 = \text{det}[Uy | Uz | x*Ux + y*Uy + z*Uz + d*Ud + W]\\ \end{align} \]
Noting that the determinant is linear in its columns as well as that a matrix with a repeated column has a zero determinant, then: \[ \begin{align} \\x = \frac{d*\text{det}[Uy | Uz | Ud] + \text{det}[Uy | Uz | W]}{\text{det}[Uy | Uz | Ux]}\\ \end{align} \]
The same method is applied to obtain y and z in terms of d:
\[ \begin{align} \\y = \frac{d*\text{det}[Ux | Uz | Ud] + \text{det}[Ux | Uz | W]}{\text{det}[Uy | Uz | Ux]}\\ \end{align} \] \[ \begin{align} \\z = \frac{d*\text{det}[Uy | Ux | Ud] + \text{det}[Uy | Ux | W]}{\text{det}[Uy | Uz | Ux]}\\ \end{align} \]
We can now subtitute our x, y, z in terms of d into the first quadratic equation of our system, thus making it a one varible equation. Using the quadratic formula results in two solutions.
Step 4
We now set up a test of the conditioning of our GPS problem. Satellite positions \((A_i,B_i,C_i)\) are defined from spherical coordinates \((\rho,\phi_i,\theta_i)\) such that: \(A_i= \rho\cos\phi_i\cos\theta_i\), \(B_i=\rho\cos\phi_i\sin\theta_i\), and \(C_i=\rho\sin\phi_i\). We define \(\rho = 26570\) km, while \(0\leq\phi_i\leq\frac{\pi}{2}\) and \(0\leq\theta_i\leq2\pi\) where \(i=1,...,4\). We then calculate the corresponding satellite ranges \(R_i= \sqrt[2]{A_i^2 + B_i^2 + (C_i - 6370)^2}\) as well as travel times \(t_i=d+\frac{R_i}{c}\), where \(c = 299792.458 \).
For our situation, we define a spefically tailored error magnification factor where the backward error is the input change in meters and the forward error is the change in position caused by such a small change in \(t_i\), also in meters. Thus, \(\text{EMF} = \frac {||(\triangle x,\triangle y,\triangle z)||_\infty}{c||(\triangle t_1,...,\triangle t_m)||_\infty}\) and the condition number is the maximum error magnification factor for all small \(\triangle t_i's\). Using this code, we arrive at the following results.
It is thus clear that our maximum position error for this step is 0.01865853, while our condition number is 6.22381437.
Step 5
We are now asked to perform the same calculations as in Step 4, only this time the satellites are bunched up to be within five percent of one another. We use this code to obtain the following results.
For this situation, we have a maximum position error of 4111.945955 and condition number of 1371597.5326. It is clear that in comparision to the satellites from Step 4, the conditioning for the bunched satelittes is much worse. We believe that this is the case due to the fact the bunched satellites seem to act as one satellite instead of four, this effect being caused by their almost identical spheres. This results in multiple points where all four spheres intersect, thus creating a potential for higher error.
We use multiNewtonGeneral.m for Steps 4 and 5.
Step 6
We look into the effect of adding additonal satellites and whether it could potentially decrease our errors and condition numbers. We add four more satellites to the configuration from Step 4 and use gaussNewton.m to solve the least squares sytem of eight equations in four variables \(x,y,z,d\). We use this code to obtain the following results:
We test intial vectors \(f_1 = (0, 0, 0, 0)\), \(f_2 = (-3, 5, 8000, .0003)\), and \(f_3 = (1000, 2000, 3000, .01)\) as well as various other guesses. All of our tested vectors converged, thus we believe that there must be infinitely many "good" initial vectors. For this step, we find the maximum position error to be 0.01093391 and the conditioning number to be 3.64716040.
Below is a summary of our results: \begin{array}{|c|c|} \hline \text{}\ & \text{4 Satellites}\ & \text{4 bunched Satellites} \ & \text{7 Satellites} \ \\ \hline \text{Maximum Position Error (km)}\ & 0.0186585260698848 \ & 4111.94595480825 \ & 0.0109339117969508 \ \\ \hline \text{Maximum EMF}\ & 6.22381436950821 & 1371597.53264126 & 3.64716039552628 \\ \hline \end{array}It must be noted that for all condition estimates and position errors, our results are very much limited by our positioning of the satellites. Therefore, our maximum EMFs in all cases are simply lower bounds on the condition number of the problem. However, through our experimentation these are our best guesses.