|
|
George Mason UniversityZakaria Tarik ZerhouniSource: Home > Classes > Math 447 > Project 1 > Step 2Math 447: Numerical Analysis
2. Plot the solution from Step 1 against the correct solution: $$y(x)=\frac{f}{24EI}x^2(x^2-4Lx+6L^2)$$ where \(f=f(x)\) is constant defined above. Check the error at the end of the beam, \(x=L\) meters. In this simple case the derivative approximations are exact, so your error should be near machine round off. The error at \(x = L\) was computed as \(-6.591949208711867e-16\). Machine epsilon, denoted as \(\epsilon_{mach} = 2^{-52}\) is the distance between 1 and the smallest floating point number greater than one. In this way it defines the bounds of computing accuracy for IEEE double precision floating point standard. As \(\epsilon_{mach} \approx 2.22e-16\), the result returned for the error at \(x = L\) is near machine round-off. 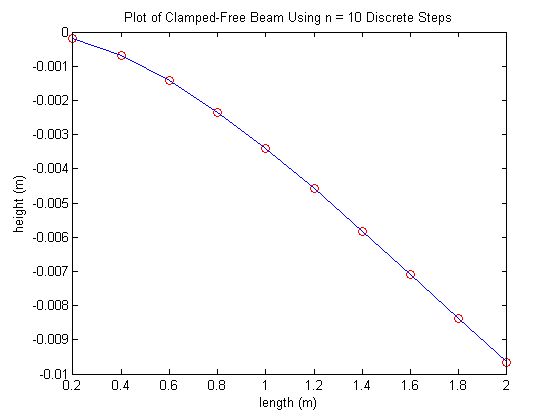
Click on picture to view the associated code.
|