|
|
George Mason UniversityConor Philip NelsonSource: Home > Classes > Math 447 > Project 4 > Step 1Math 447: Numerical Analysis
Example 8.12 (pg. 419): Use the Backward Difference Equation with Newton iteration to solve Burgers' equation. This utilizes burgers.m code to compute when \(\alpha=5\) and \(\beta=4\). Consider the following: \[f(x,t)= \begin{cases} u_t +uu_x=Du_{xx} & \\ u(x,0)=\frac{2D\beta\pi\sin(\pi x)}{\alpha + \beta\cos(\pi x)} & \text{for } 0 \leq x \leq 1\\ u(0,t)=0 & \text{for all } t \geq 0\\ u(1,t)=0 & \text{for all } t \geq 0 \end{cases} \] With burgers(0,1,0,1,20,40), we have: 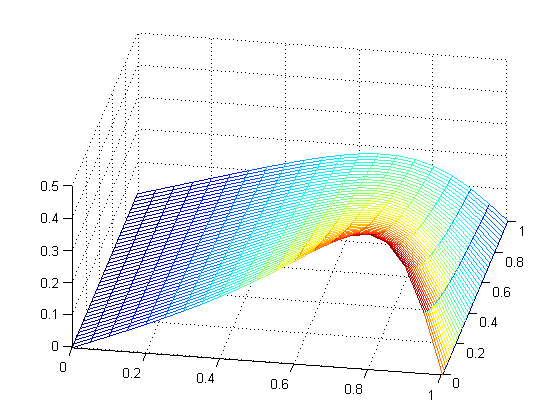
|