George Mason University

Conor Philip Nelson

(8.4.2) Solve Burgers’ equation on the interval [0,1] with homogeneous Dirichlet boundary conditions and the initial condition given in (8.66) with parameters \(\alpha=4\), \(\beta=3\), and \(D=0.2\). Plot the approximate solution using step sizes \(h=0.01\), \(k=\frac{1}{16}\), and make a log-log plot of the approximation error at \(x=\frac{1}{2}\), \(t=1\) as a function of \(k\) for \(k=2^{-p}: p=4,5,...,8\).

---

---

For part 4 we proceeded using the specifications in the problem, and obtained a graph of the approximate solution corresponding to a step size in the time dimension of k=1/16, which is displayed below. We utilized burgers 8.4.2.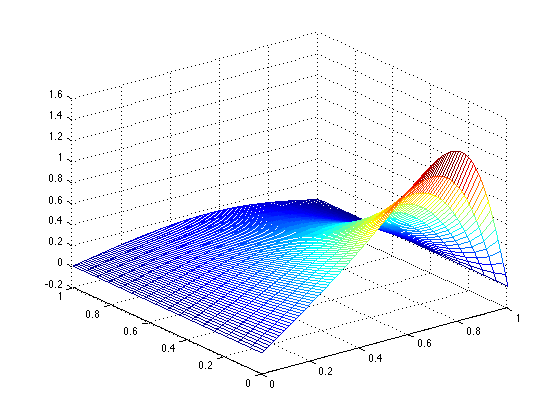



Using the exact solution for the Burgers' equation provided in the text, we then calculated approximate solutions with more granularity in the time step, and compared the exact solution to approximation in order to estimate error as a function of step size. At \((x,t)=(1/2,1)\) we calculated the following error values, which are featured in the following log-log plot. As expected from the Backward Difference Method, we can see a roughly first-order decrease in error as a function of time step size, due to the fact that the error from the time step dominates the error from the spatial step.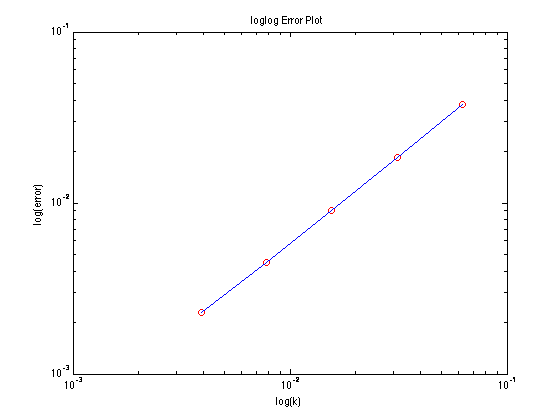

Previous: Step 3

Project 4 Home