|
|
George Mason UniversityConor Philip NelsonSource: Home > Classes > Math 447 > Project 4 > Step 3Math 447: Numerical Analysis
(8.4.1) Solve Burgersí equations (8.63) on [0,1] with initial condition\( f(x)=\sin(2x\pi)\) and boundary conditions \(l(t)=r(t)=0\), using step sizes: (a) \(h=k=0.1\) (b) \(h=k=0.02\) Plot the approximate solutions for \(0 \leq t \leq 1\). Which equilibrium solution does the solution approach as time increases? We will utilize burgers.8.4.1.m for this problem. Consider Burger's equation with Dirichlet boundary conditions: (8.63) \[f(x,t)= \begin{cases} u_t +u*u_x=Du_{xx} & \\ u(x,0)=f(x) & \text{for } x_l \leq x \leq x_r\\ u(x_l,t)=l(t) & \text{for all } t \geq 0\\ u(x_r,t)=r(t) & \text{for all } t \geq 0\ \end{cases} \] (a) When \(h=k=0.1\). We have: 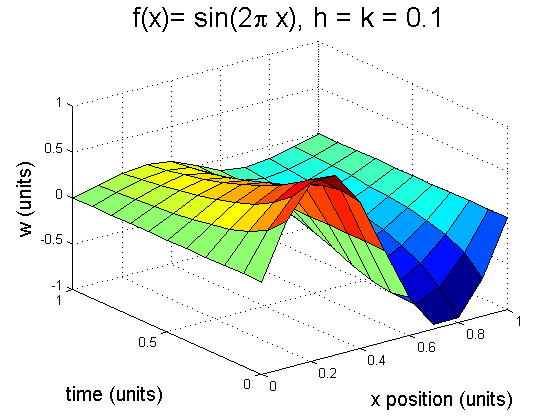
(b) When \(h=k=0.02\). We have: 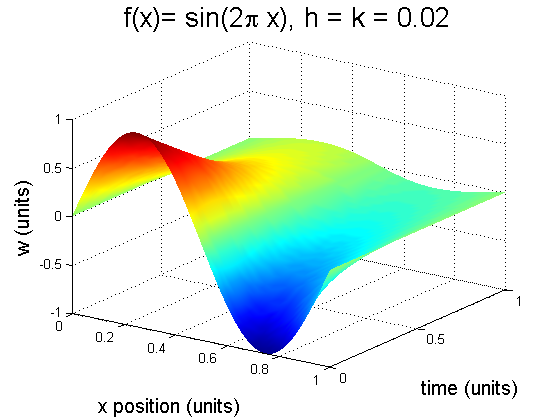
It is clear to note that with this \(k\) value, these mesh lines are so close together that it causes a skew of vision where there will be blackness overtaking the depictions. Hence as to why we used the \(shading\) interpretion. Note that as time increases, \(x\) goes to 0: 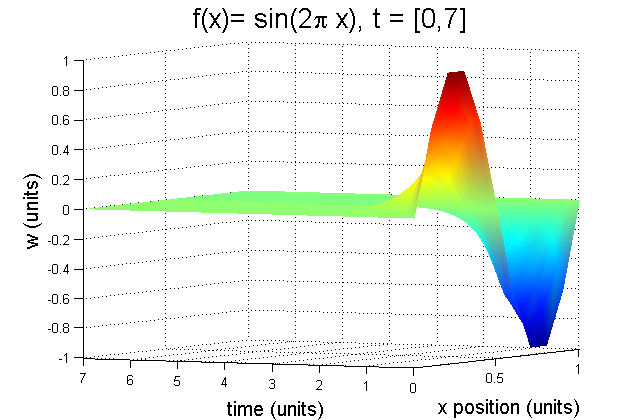
|