George Mason University

Conor Philip Nelson

(Exercise 8.4.3) Show that the function \(u(x,y)\) in (8.68) is a solution of the Burgers’ equation with Dirichlet boundary conditions (8.66)

---

---

(8.66) Burgers' equation: \[f(x,t)= \begin{cases} u_t +uu_x=Du_{xx} & \\ u(x,0)=\frac{2D\beta\pi\sin(\pi x)}{\alpha + \beta\cos(\pi x)} & \text{for } 0 \leq x \leq 1\\ u(0,t)=0 & \text{for all } t \geq 0\\ u(1,t)=0 & \text{for all } t \geq 0 \end{cases} \] Note there is not always an analytical solution to a PDE, however we are given one in the text. $$u(x,t) = \frac{2D\beta\pi e^{-D \pi^2 t} \sin(\pi x)}{\alpha+\beta e^{-D \pi^2 t}\cos(\pi x)}$$ To verify that this is a solution, we must reduce this equation to that of the initial and boundary conditions. [Here are the written solutions: 1, 2 and 3.] $$ u(x,0) = \frac{2D\beta\pi e^{-D \pi^2 (0)} \sin(\pi x)}{\alpha+\beta e^{-D \pi^2 (0)}\cos(\pi x)}=\frac{2D\beta\pi \sin(\pi x)}{\alpha+\beta\cos(\pi x)} $$ $$ u(0,t) = \frac{2D\beta\pi e^{-D \pi^2 t} \sin(\pi (0))}{\alpha+\beta e^{-D \pi^2 t}\cos(\pi (0))}= 0 $$ $$ u(1,t) = \frac{2D\beta\pi e^{-D \pi^2 t} \sin(\pi (1))}{\alpha+\beta e^{-D \pi^2 t}\cos(\pi (1))}= 0 $$ We begin by simplifying both the numerator and denomenator of the initial equaion: $$ u(x,t) = \frac{2D\beta\pi e^{-D \pi^2 t} \sin(\pi x)}{\alpha+\beta e^{-D \pi^2 t}\cos(\pi x)} $$ $$ =\frac{M}{N} $$ We must find \(u_x\), \(u_{xx}\) and \(u_t\). We have:

For \(u_x\): $$ u_x=\frac{NM_x-MN_x}{N^2} $$ $$ =\frac{2 \beta D \pi^2 e^{-D \pi^2 t} (\alpha e^{2 D \pi^2 t} \cos(\pi x)+\beta e^{D \pi^2 t})}{(\alpha e^{D \pi^2 t}+\beta \cos(\pi x))^2} $$ For \(u_{xx}\): $$ u_{xx}=\frac{N^2M_{xx}-MNN_{xx}-2NM_xN_x+2MN_x^2}{N^3} $$ $$ = \frac{(4 \beta^2 D \pi^3 e^{-D \pi^2 t} \sin(\pi x)) (\alpha e^{2 D \pi^2 t} \cos(\pi x)+\beta e^{D \pi^2 t})}{(\alpha e^{D \pi^2 t}+\beta \cos(\pi x))^3}-\frac{2 \alpha \beta D \pi^3 e^{D \pi^2 t} \sin(\pi x)}{(\alpha e^{D \pi^2 t}+\beta \cos(\pi x))^2} $$ For \(u_t\): $$ u_t=\frac{NM_t-MN_t}{N^2} $$ $$ = \frac{2 \beta^2 D^2 \pi^3 \sin(\pi x) \cos(\pi x)}{(\alpha e^{D \pi^2 t}+\beta \cos(\pi x))^2}-\frac{2 \beta D^2 \pi^3 \sin(\pi x)}{(\alpha e^{D \pi^2 t}+\beta \cos(\pi x))} $$ Now that we will plug in the individual components. We will evaluate the expression with respect to \(u_{xx}\). We have: $$ \frac{u_t+uu_x}{D} = \frac{N^2M_t+MN(M_x-N_t)-M^2N_x}{N^3D} $$ Which simplifies to: $$ =\frac{N^2M_{xx}-MNN_{xx}-2NM_xN_x+2MN^2_x}{N^3} $$ Which is equivalent to \(u_{xx}\). Therefore, verifying that this solves the Burgers' equation.

Finally via (burgers 8.4.3), heres the exact solution: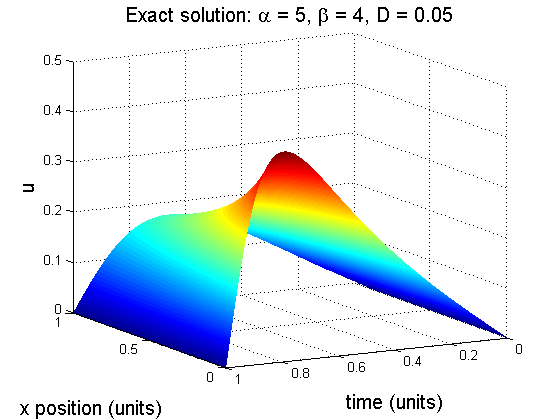

Project 4 Home

Next: Step 2