Simple Denoising Methods

Part XIV: Denoising by Sobolev and Total Variation Regularization

First we discuss image prior's and regularization. Mr. Peyrê defines an image prior as the following:

"For a given image $f$ , a prior $J(f)\in \mathbb{R}$ assigns a score which is supposed to be small for the image of interest." (1) These priors can be used in denoising via the following formula:

$min_f\frac{1}2\left \| y-f \right \|{}^2 + \lambdaJ(f)$

"A denosing of some noisy image $y$ is obtained by a variational minimization that mixes a fit to the data (usually using an $L^2$ norm) and the prior. If $J(f)$ is a convex function of $f$ , then the minimum exists and is unique." (2) Next Mr. Peyrê introduces another parameter, $\tau$ , to this process. "The parameter $\tau > 0$ should be adapted to the noise level. Increasing it's value means a more aggressive denoising. If $J(f)$ is a smooth functional of the image $f$ , a minimizer of this problem can be computed be gradient descent. It defines a series of images $f^{(l)}$ indexed by $l\in \mathbb{N}$ as

$f^{l+1}=f^{(l)}+\tau(f^{(l)}-y+\lambda\nabla J(f^{(l)}))$ (3)"

It turns out that the necessary requirements for this process is work is that $J(f)$ is twice differentiable.

Sobolev Prior

Now we get to see our first type of image prior - the Sobolev Prior. The Sobolec Prior is defined as:

$J(f) = \int \left \| \nabla f(x) \right \|^2dx$

The gradient vector here a point x is defined in the following manner:

$\nabla f(x) = (\frac{\partial f(x)}{\partial x_1},\frac{\partial f(x)}{\partial x_2})$

In a discrete image of pixels, the gradient is calculated using the finite difference method. With this in mind, Mr. Peyrê loads the familiar hibiscus image and calcualtes the gradient of the image, as well as the absolute values of the gradient.

Heat Regularization for Denoising

In the words of Mr. Peyrê, "Hear regularization smoothes the image using a low pass filter. Increasing the value for $\lambda$ increases the amount of smoothing." (4) Mr. Peyrê then proceeds to add some noise to the clean hibiscus image. Sobolev regularization is performed via the Fourier Transform. Mr. Peyrê gives the following equation:

$\hat f^*(w)=\frac{\hat y(w)}{1+ \lambda S(w)}\: \: \: where \: \: S(w)=\left \| w \right \|^2$

"This shows that $\hat f^*$ is a filtering of $y$ ." (5) Here is the resulting denoising.

Next, in typical fashion, Mr. Peyrê iterates through many values for $\lambda$ in order to determine which value is best.

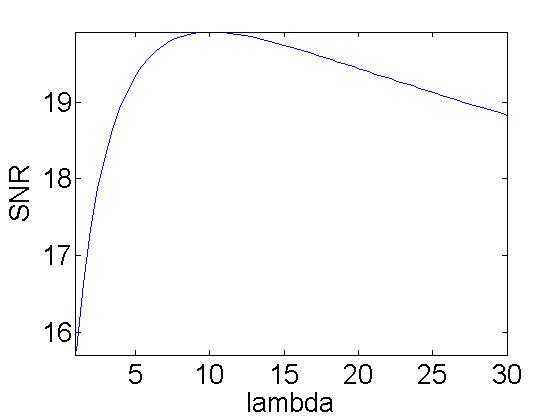
Here is the denosing with the optimal value for $\lambda$ :

Total Variation Prior

Works Cited

(1) Peryê, Gabriel. "Denoising by Sobolev and Total Variation Regularization." Denoising by Sobolev and Total Variation Regularization. N.p., 2010. Web. 18 Aug. 2014. .

(2) Peryê, Gabriel. "Denoising by Sobolev and Total Variation Regularization." Denoising by Sobolev and Total Variation Regularization. N.p., 2010. Web. 18 Aug. 2014. .

(3) Peryê, Gabriel. "Denoising by Sobolev and Total Variation Regularization." Denoising by Sobolev and Total Variation Regularization. N.p., 2010. Web. 18 Aug. 2014. .

(4) Peryê, Gabriel. "Denoising by Sobolev and Total Variation Regularization." Denoising by Sobolev and Total Variation Regularization. N.p., 2010. Web. 18 Aug. 2014. .

(5) Peryê, Gabriel. "Denoising by Sobolev and Total Variation Regularization." Denoising by Sobolev and Total Variation Regularization. N.p., 2010. Web. 18 Aug. 2014. .

G. Peyré, The Numerical Tours of Signal Processing - Advanced Computational Signal and Image Processing, IEEE Computing in Science and Engineering, vol. 13(4), pp. 94-97, 2011.