Simple Denoising Methods

Part XIII: Linear Signal Denoising

Again, we take a signal and "corrupt" it by adding some Gaussian white noise to it. This is given by the equation: $y = x_0 + w$ The plot of the original and corrupted signal are given below.

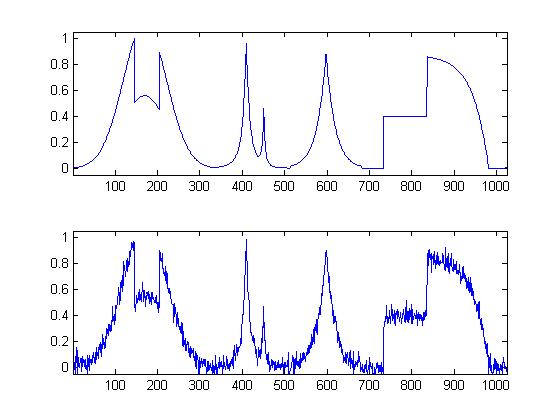
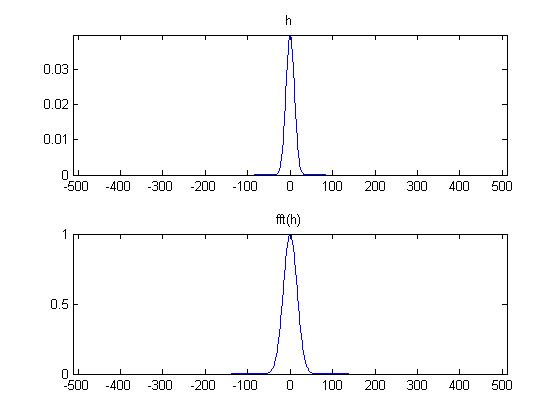
Now we attempt to perform Linear Signal denoising on the corrupted signal. This process involves our observation of the output vector y. "A translation invariant linear denoising is a convolution with a kernel h." (1) This is given by the equation: $x = x_0\star h$ . The filter h is a Gaussian that is determined by a parameter $\mu$ . Of course, we know that convolution in the time domain is tantamount to multiplication in the frequency domain, so one can perform the operation above in the frequency domain as well. By moving the paramter $\mu$ around, one can see varying degrees of Linear Signal denoising. The plot of the filter h is given below.

Below is the result of our first attempt at Linear Signal denoising.

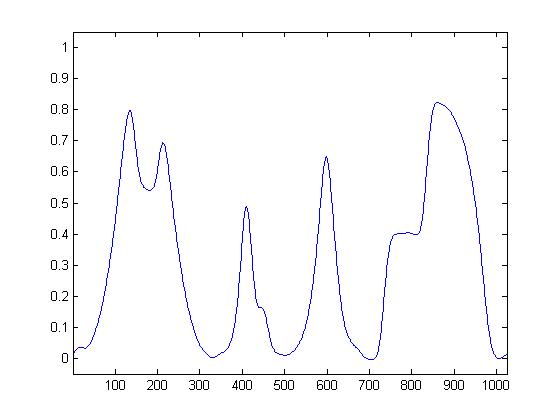
As one might notice, the edges of the original signal have been smoothed out a great deal. Can we do better? Absolutely. Mr. Peyrê implements an iterative method where he cycles through different values for $\mu$ .

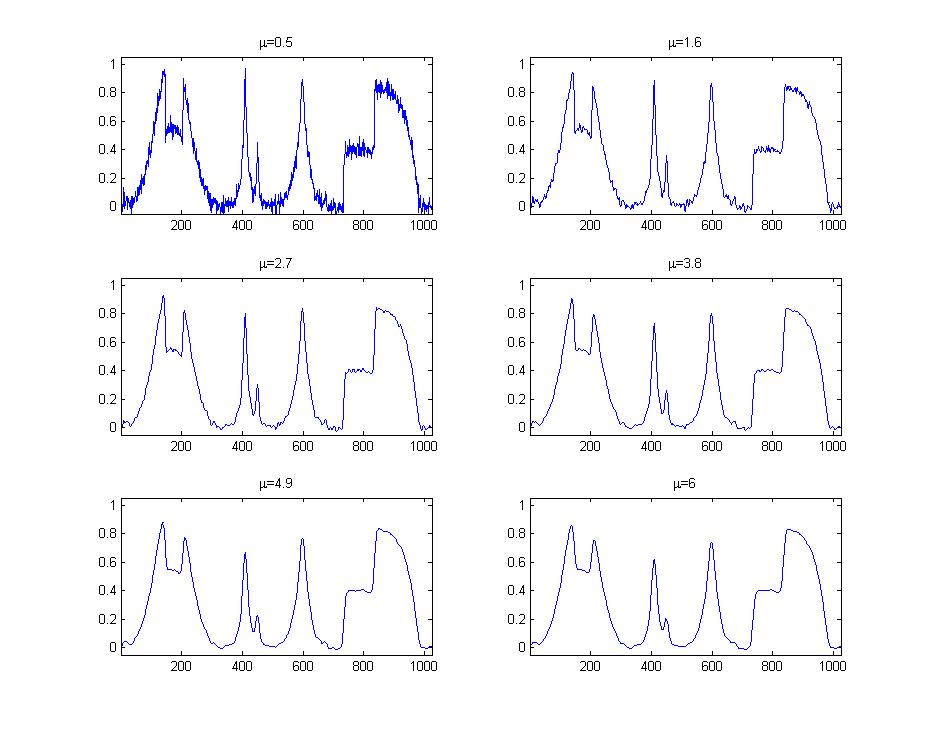
Next we show the difference between $\left \| y-x_0 \right \|$ as a function of $\mu$ . In other words, what value of $\mu$ gives us the least error? The plot is given below.

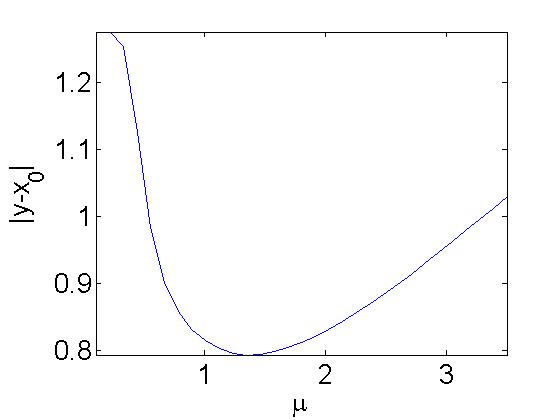
The value of 1.3467 for $\mu$ gives us the best denoising of the original signal. The result is given below.

Wiener Filtering

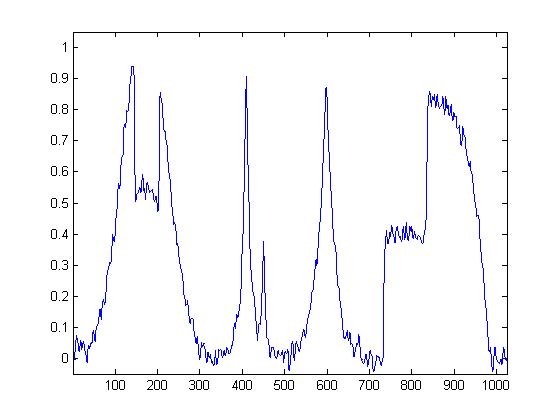
Here again we consider $x_0$ . In the words of Mr. Peyrê, "We suppose here that $x_0$ is realization of of a random vector $x_0$ , whose distribution is a Gaussian with a stationary covariance c, and we denote $P_{X_0}=\hat c(w)$ the power spectrum of $x_0$ . (2) Mr. Peyrê proceeds to give the "oracle optimal filter" that minimizes the "risk." The equation for this filter is:

$R(h) = \varepsilon _{W,X_0}( \norm{ X_0 - h \star (X_0 + W) }^2 ).$

It turns out that the solution to this "oracle optimal filter" is the Wiener Filter. It is given by the equation below:

$\forall w\om, \quad \hat h(w\om) = \frac{ P_{X_0}(w\om) }{ P_{X_0}(w\om) + \sigma^2 }.$

Where $\sigma$ is the variance of the noise.

Mr. Peyrê proceeds to attempt an approximation to the Wiener Filter. $P_{X_0}$ is approximated by:

$P_{X_0}\thickapprox \frac{1}{N}\left | \hat x_0 \right |^2$

Here is our approximation to the Wiener Filter:

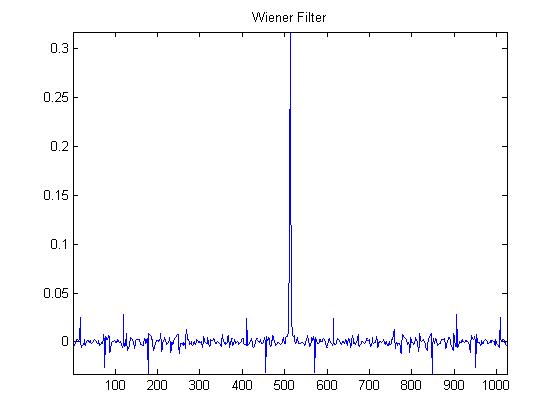
Here is the resulting denoising:

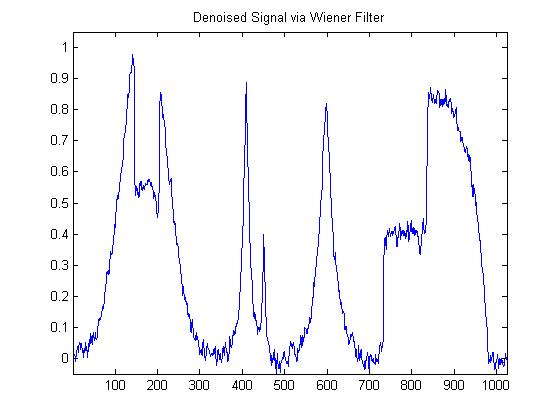
This result is extremely similar looking to the previous denoising methoid. They are almost indistinguishable. Upon close examination, the denosing with the Wiener Filter is slightly better in my book. The level of noise is ever-so-slightly less in the Wiener Filter denoising.

Conclusion

This section showcased two methods for denoising a signal. In both instances Mr. Peyrê designed a filter that attempted to remove the noise from the signalI found both methods implemented by Mr. Peyrê to be very interesting, particularly the Wiener Filter. I have a feeling that deriving the solution to the "oracle optimal filter" is quite difficult. . In the next section he does some denoising with the hibiscus which should be pretty fun.

Home

Linear Image Denoising

Works Cited

(1) Peryê, Gabriel. "Linear Signal Denoising." Linear Signal Denoising. N.p., 2010. Web. 12 Aug. 2014. .

(2) Peryê, Gabriel. "Linear Signal Denoising." Linear Signal Denoising. N.p., 2010. Web. 13 Aug. 2014. .

G. Peyré, The Numerical Tours of Signal Processing - Advanced Computational Signal and Image Processing, IEEE Computing in Science and Engineering, vol. 13(4), pp. 94-97, 2011.