|
|
George Mason UniversityConor Philip NelsonSource: Home > Classes > Math 447 > Project 1 > Step 6Math 447: Numerical Analysis
6. Now remove the sinusoidal load and add a 70 kg diver to the beam, balancing on the last 20 cm of th beam. You must add a force per unit length of \(-g*\frac{70}{.2} \frac{kg}{m}\) to \(f(x_i)\) for all \(1.8\leq x \leq 2\), and solve the problem again with the optimal value of \(n\) found in Step 5. Plot the solution and find the deflection of the diving board at the free end. In order to add the weight of the diver to the beam, the force term was modified. The sinusoidal load was removed and the linearly spaced vector \(x\) had a new term \(s\) added to it and modified as follows: \(s(x) = \left\{ \begin{array}{lr} -480wdg & : x < 1.8\\ -480wdg -\frac{70}{0.2}g & : x \geq 1.8 \end{array} \right.\) If \(x\) was greater than or equal to 1.8, the corresponding \(s\) term became the force per unit length term for the diver, otherwise, the corresponding \(s\) term became \(0\). This \(s\) vector was then added to the force vector resulting from the weight of the beam. The system of equations was then solved as before. The deflection at \(x = L\) was \(-0.2034\) meters. Figure (6.1) 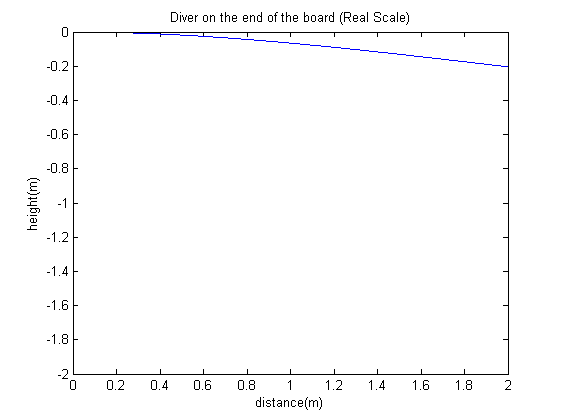
Click on picture to view the associated code. Figure (6.2) 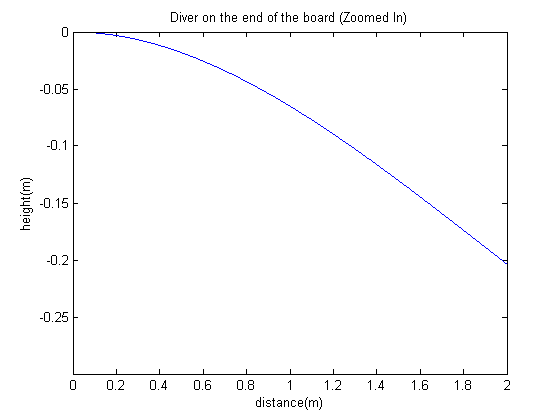
Click on picture to view the associated code.
|