---

Main Goal:

To design the dimensions of the fin to keep the temperature within safe tolerances.

---

Methods/Equations:

reality check 8
1) Finite difference approximation
2) Robin boundary condition
3) Initial condition

---

Step 1

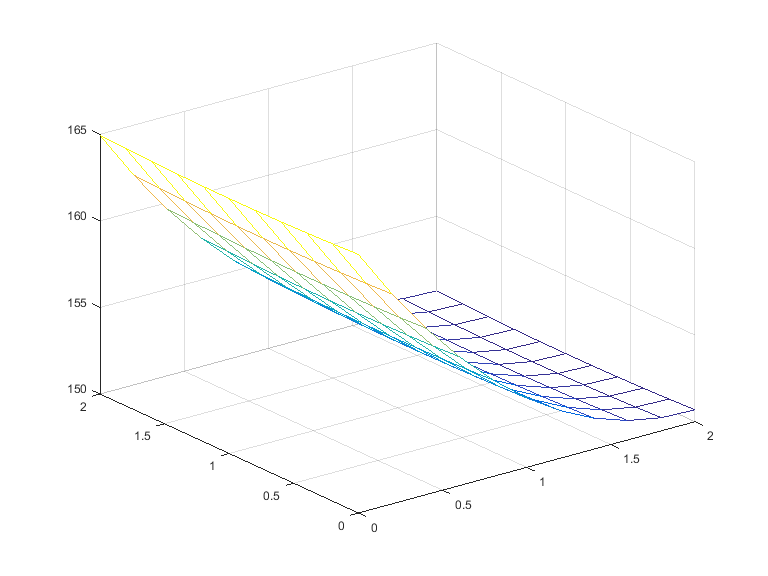
Assume: 1) Size of a fin: dimensions \(2 \times 2 cm\), with \(1 mm\) thickness.
2) Power input: \(5W\) along the entire left edge (\(2 cm\)).
3) \(M = N = 10\) steps in the \(x\) and \(y\) directions.
4) \(K = 1.68W/cm°C\)(aluminum fin),   \(H = 0.005W/cm2 °C\),   \(u_b = 20 °C\).

Goal: Plot the resulting heat distribution over the xy-plane (Use the mesh command),
and determine the maximum temperature(°C) of the fin.

Matlab code: here

Result: Maximum temperature = 1.649356799942613e+02 °C

---

Step 2

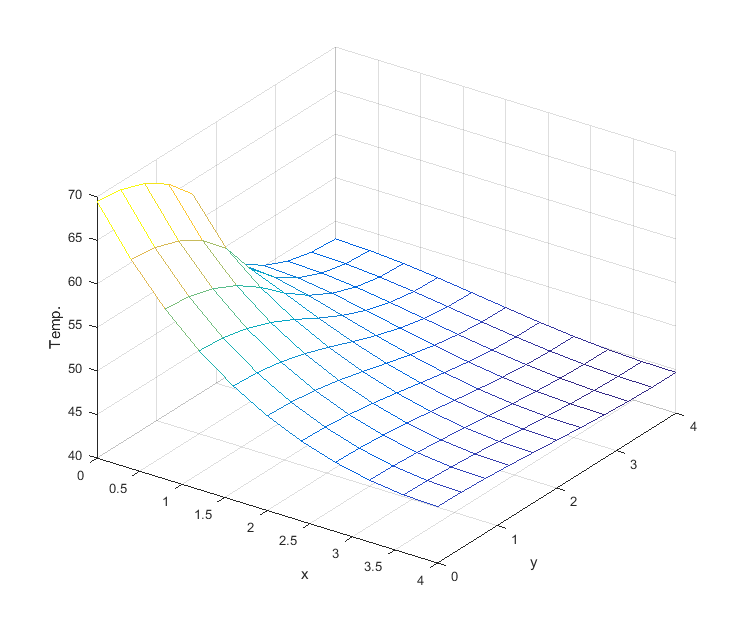
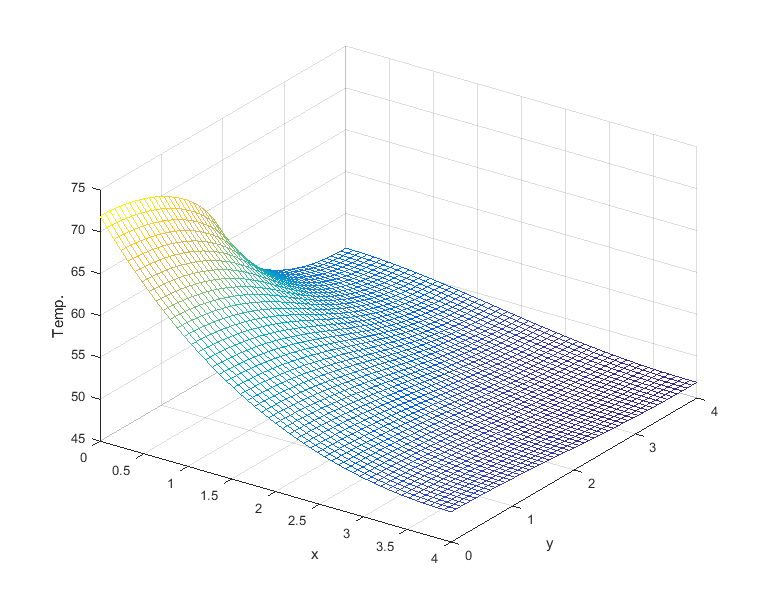
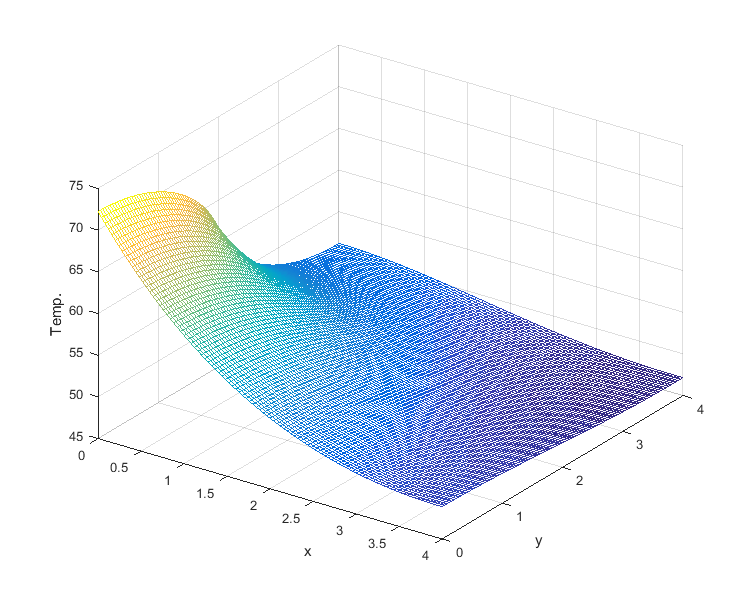
Assume: 1) Size of a fin: dimensions \(4 \times 4 cm\), with \(1 mm\) thickness.
2) Power input: \(5W\) along the interval \([0,2]\) on the left side (\(2 cm\)).

Goal: Plot the resulting heat distribution,
and find the maximum temperature(°C).
Experiment with increased values of M and N.

Matlab code: here

Result:

	N=M=10 maxT = 69.470375461811372 gap from N=100 = 2.7693 (3.83%)	N=M=50 maxT = 71.898570423874901 gap from N=100 = 0.3411 (0.47%)	N=M=100 maxT = 72.239674205733081

---

Step 3

Assume: 1) Size of a fin: dimensions \(4 \times 4cm\), with \(1 mm\) thickness.
2) Power input: \(5W\) along the interval \([0,2]\) on the left side (\(2 cm\)).

Goal: Use a "for" loop to find the maximum temperature(°C) at some interval of power.
Compare the maximum temperature at each power
and select the highest power that keeps the maximum temperature below 80(°C).

Matlab code: code1   code2

Result: Maximum power that keeps the maximum temperature below 80(°C) = 5.79 W

---

Step 4

Assume: 1) Size of a fin: dimensions \(4 \times 4cm\), with \(1 mm\) thickness.
2) Power input: \(5W\) along the interval \([0,2]\) on the left side (\(2 cm\)).
3) The thermal conductivity K=3.85 W/cm°C(copper fin)

Goal: Use a "for" loop to find the maximum temperature(°C) at some interval of power.
Compare the maximum temperature at each power
and select the highest power that keeps the maximum temperature below 80(°C).

Matlab code: code1  code2

Result: Maximum power that keeps the maximum temperature below 80(°C)
i) power input place \([0,2]\): 7.32W
ii) power input place \([1,3]\): 7.64W

Result: Aluminum fin vs. Copper fin

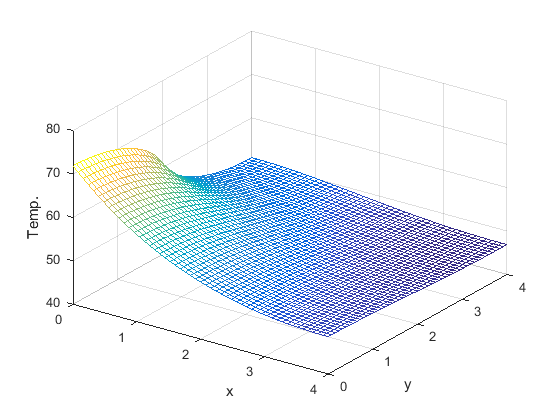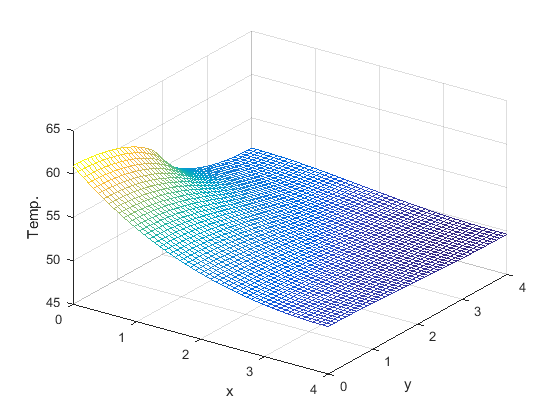	K=1.68W/cm°C(aluminum fin) Power input 5W	K=3.85 W/cm°C(copper fin) Power input 5W

---

Step 5

Assume: 1) Size of a fin: dimensions \(4 \times 4cm\),, with \(1 mm\) thickness.
2) Power input: \(5W\) along the interval \([0,2]\) on the left side (\(2 cm\)).

Goal: Use a nested "for" loop to find the maximum temperature(°C)
at some interval of power and some value of K. Compare the maximum temperature
at each power and select the highest power that keeps the
maximum temperature below 80(°C). Then plot a function of K vs. P.

Matlab code: here

Result: data

---

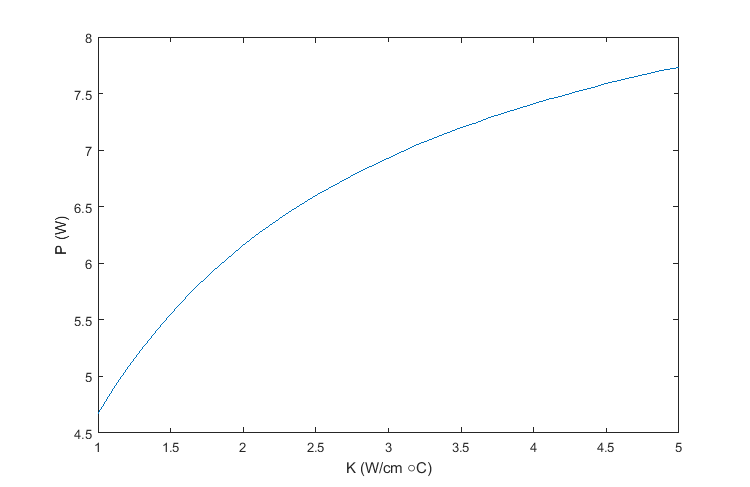
Step 6

Assume: 1) Size of a fin: dimensions \(4 \times 4cm\), with \(1 mm\) thickness.
2) Power input: \(5W\) along the interval \([0,2]\) on the left side (\(2 cm\)).
3) The thermal conductivity K=3.85W/cm(°C)
4) The heat transfer coefficent \(H=0.1W/cm^2\)(°C)

Goal: Use a "for" loop to find the maximum temperature(°C) at some interval of power.
Compare the maximum temperature at each power
and select the highest power that keeps the maximum temperature below 80(°C).

Matlab code: here

Result: Maximum power that keeps the maximum temperature below 80(°C)= 36.75 W