Artificial intelligence computation, however, does not fit well into an input-grind-output format. "Reversible agents" should run indefinitely, observing their world, acting to achieve goals, and talking with other autonomous agents. Do these additional requirements introduce more intrinsic entropy costs for such agents?
This preliminary survey suggests that they do. Goal states can unavoidably have lower entropy than initial states. Sensing costs, when features of the world relevant to an agent's analysis change unpredictably before the agent has time to reverse that analysis. On the other hand, talk between nearby agents can be cheap.
In artificial intelligence, however, "computation" can invoke images of autonomous agents trying to achieve goals and survive indefinitely, using finite computer hardware to continuously coordinate their observations, actions, and communications. Thus we may wonder: What if any additional entropy costs must such agents pay to go about their business?
After reviewing the general concept of reversible computation, this paper will describe several different types of fundamental entropy costs that agents must apparently pay, including costs to achieve goals states, to observe a changing world, to run indefinitely in finite memory, and to exchange messages with other agents. Each kind of cost will be described in turn and then these costs will be compared.
The largest cost appears to be that of measuring a world whose relevant features might change before the agent can reverse all the computation which depended on that feature. Should a more careful analysis confirm their existence, such costs may be a dominant fundamental physical limit to useful "computation".
Thus, to decrease the "entropy", or (logarithm of) number of possible states, of one system, one must increase the entropy of some other system by at least the same amount. And since these mappings can easily get so complex that one loses track of exactly which states map onto which, in practice the total entropy can increase.
The fact that total entropy never decreases fundamentally limits the kinds of useful things one can do in the world. For example, a gear rotating against friction maps simple initial rotations onto many possible resulting vibrations. And to refrigerate one volume, one must typically heat some other volume. Without "negentropy", or the potential to increase the entropy of some system, one can do very little. With negentropy, one can do most anything possible: collect energy and matter, or arrange and sort it in complex ways.
Historically, computer devices have been designed without close attention to entropy loses. For example, a typical "and" gate maps four possible input signals (two bits) to two possible outputs (one bit), clearly not a one to one map (one bit lost). But recently it has been shown that such losses are not intrinsic to computer logic; "reversible" (one to one) gates can be designed with no logical losses, and with bits of entropy lost to friction per instruction inverse in the time allowed to execute each instruction at low temperature.
There are also no intrinsic entropy costs associated with a computer slowly measuring a static external system. While observations may allow a "Maxwell's demon" to reduce the entropy of the world around it, it must pay a compensating number of bits to internally record this data. Eventually a finite memory demon must either undo this entire operation, returning the demon and the world to their initial entropy levels, or it must pay entropically to erase this data (a many to one map).
The number of bits required to store a measurement is, on average, given by the the log (based two) of the agent's prior estimated probability of measuring this value. The number of bits of entropy an agent must "waste" to erase some data is given by the probability the agent would guess, after the erasure, that this was the information erased.
While such reversible computer designs are not currently practical, it is only a matter of time before they become dominant. Average bits of entropy lost per logic operation has decreased a factor of ten every five years for many decades, and should go below one by the year 2015 [3]. Since we will probably not have human-level artificial intelligence by this time, it is perhaps reasonable to consider the case examined in this paper, that of intelligent robots running on reversible computer hardware, being very careful about the number of bits they waste.
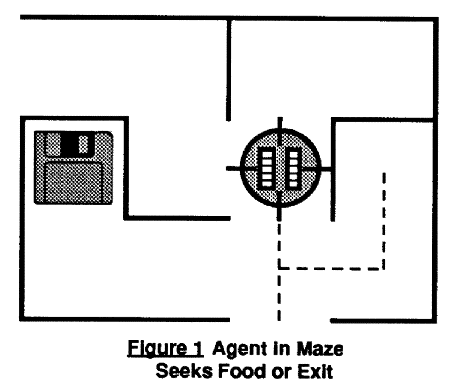
To see all this in more detail, and to set the stage for understanding other costs, let us consider the particular agnet environment shown in Figure 1, and compare the costs to achieve several different possible tasks. In this, a robot wanders a static maze, where walls rising from the borders of a two-dimensional grid of squares. Imagine grooves in the floor allow the robot to reversibly move forward or back one square or to rotate a quarter turn in either direction. And imagine the robot has four sensing rods which can probe for the existence of a wall in each of the four cardinal directions, each rod being a one-bit measuring instrument switched in the usual way between bistability and monostability. For concreteness, one may image the agent's CPU to be implemented in reversible rod logic [4], where state is held in the position of short solid rods. This allows a particularly simple interface between the CPU and its sensors.

What if the agent's goal was to find and eat some sort of food in the maze, say blank tape that the agent could write garbage bits into? Then if the agent were sure that it would find food, it need pay no entropy costs. While wandering the maze it might remember every measurement it took. Once the agent had found and eaten the food, it could then reverse its path, undoing each measurement it had made and eventually returning to its starting point. The agent would then know that it had eaten, but would not remember where it ate.
If, however, the agent wanted to remember something about where it ate, so as to avoid looking there for food next time, it would have to pay to encode that information to the degree of spatial precision desired. The farther it wandered away, the less spatial precision it would probably desire, but the harder it might be to unlearn that knowledge. As a primary goal, knowledge can cost; as a subgoal it may or may not cost.
What if the agent's goal in searching the maze was to find an exit, in order to escape the maze? In this case it might find the exit and then retrace its steps, remembering only a minimal set of instructions for getting to the exit from where it started without looking at anything. Then it could just head for the exit and be out. If the agent wants to remain outside the maze, however, it seems the agent must pay to remember (or erase) at least part of these minimal instructions.
In general, agents may desire to achieve goal states which are low entropy, or which unavoidably embody information about the world. If different possible evidence about the world would lead to different ways of achieving a goal, and thus different resulting goal states, then one must pay to encode that evidence.
An agent's goal costs depend of course on the kind of goals that agent adopts. But one common subgoal must surely be to regularly obtain some sort of entropic food to offset entropic losses.
For example, if the maze walls in Figure 1 move unpredictably, then an agent trying to undo its search by retracing its steps would run the risk that the path had changed, and thus it might have to search around to connect back with the path it remembered. Such an agent might be stuck paying to encode the old (now invalid) path segment.
In general, whenever one remembers a past which is not totally inferable from what one can see at present, one is stuck paying for the difference. This cost depends in the usual way on the probability one would assign to the past having been that way, given everything else one knows or can observe at present.
If all wall jumps were internal to the maze, and followed a known deterministic law depending only on the positions of other walls, and if the agent knew the entire maze, then in principle no bits need be wasted while traveling. The agent could just repeatedly update its internal description of the maze by projecting the maze's evolution in time, and thus never be surprised by what it sees. However, in practice small uncertainties about the mazes state or its evolution laws can quickly compound into wholesale uncertainty about the maze; knowledge can help reduce, but not eliminate, the costs of change.
How much the agent pays for the maze changing depends on both the average time between wall jumps and the average time the agent delays before trying to undo its measurement. In general, an agent could have less changing data costs if it just increased its clock speed, but this would presumably cost in increased friction losses.
However, even when an agent can't slow down the world, it may be able to speed up its use of information about that world. For example, when an agent realizes it has reached a maze dead-end, it could undo its measurements immediately as it backed out of that dead end, and just remember a dead-end tag at path's entrance. When all paths from a choice point had all dead-end tags, those tags could be undone and replaced with a tag at the entrance to the path leading to that choice point, as so on recursively.
Upon reaching the goal the agent would only remember a single path back to the start, and dead-end tags on some of the paths leading from that path. Returning back along this path, the agent could then try to reverse its inferences of each remaining dead-end tags. Even if the maze changed rapidly, the agent need not pay much for this change if the status of paths as dead-ends (or not) didn't often change.
In general one wants to quickly compute concise stable features from voluminous ephemeral data, so that one can reverse the computation of those features before the data changes. Such features cost less to erase, and are less likely to need erasing. Other examples of this approach are using many position probes to learn the detailed shape of a wall, which is then summarized as a certain type of wall, or using many motion probes down to a vibrating floor to conclude how floppy the floor is, without recalling specific motion values.
Measurement costs clearly depend on the kind of world an agent lives in. But if agents are to get along in a world anything like our own, these costs are likely to be substantial.
One can construct a single reversible computing "unit" by taking a reversible CPU (built from reversible gates), saving a history of the result of executing each CPU instruction, and then reversing this process after saving the final cycle output. We can say that such a unit takes a perhaps very large input "register" and uses it to replace a blank output register with an specific output, returning the input as it was. All this is done in one "unit cycle", a time set so as to be about the time required to copy one register into another.
Irreversibly, one could just use this one unit repeatedly to compute, overwriting the input each cycle. But Bennett has shown that this same unit can be used to reversibly simulate such an irreversible computation. If a total problem output could be irreversibly computed from a problem input in T cycles and using a register of size S, then the same problem can be computed reversibly in time linear in T, and space of order O(STa), where a can be made arbitrarily small. To do this, Bennett uses a recursive approach with n levels of recursion and a branching of k at each level.
If one tried to implement an indefinitely running agent by letting T go to infinity, Ta would eventually blow up, requiring arbitrarily large space to simulate a given finite space irreversible computation. With any finite rate of bit waste due to other causes, there is no point in going to logical extremes to reduce this source. Instead I imagine the scenario sketched in Figure 2, where agents choose some "grand period" and erase one register every period. Before throwing out a register, it is of course best to try and compress it as well as possible relative to the oldest other register one holds.
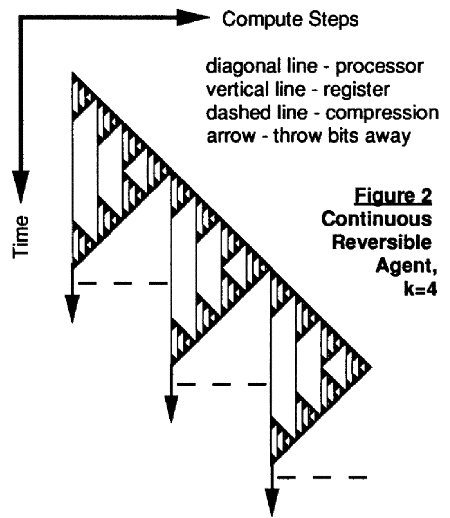
To support a constant running speed, I prefer a parallel analogue to Bennett's scheme, using 2n computing units, each with k external registers (one for input, one for output, and the rest for managing the recursion), to reversibly simulate one irreversible unit at about the same speed. Each unit handles one level of recursion, and the factor of two comes from having two sets of units, so that one set is always computing forward, while the other set reverses previous computation. The grand period would then be kn basic cycles long.
This design needs to be modified to accommodate measurements of a changing world. Separate modules should quickly summarize ephemeral data into concise features, and then reverse the measurement of that data. If there is any chance that these features will change over a grand period, such features must be cached over this time to allow the later reversal of computation that depended on those features. If, as seems likely, features needing to be cached arrive at some constant rate, then the space requirements of this cache will dominate if the grand cycle time is too long. And when there is some rate at which features become no longer true of the world, agents will have to pay to forget changed features no longer of interest. I suspect that such costs will dominate for agents with a familiar interest in the world around them.
It depends on how much time messages spend in transit. If message delay is longer than a grand period, then either the receiver or the sender must always pay for the message. At the other extreme, if the two agents follow the same n,k recursion schedule, and only send messages to arrive before the next turnaround point of the lowest recursion level (always less than k times the basic compute cycle away), then they can send and unsend without problems.
An intermediate approach, sketched in Figure 3, is for agents to cache all the messages they send or receive, and to just coordinate on having about the same length grand periods starting at about the same time. This allows agents to send and unsend each message just once, without coordinating the details of their reversing recursion. In every recursion but the first send and the last unsend, other computation just interacts with the cache as if it were the other agent. Agents would of course need to avoid talking near the very end of a grand period.
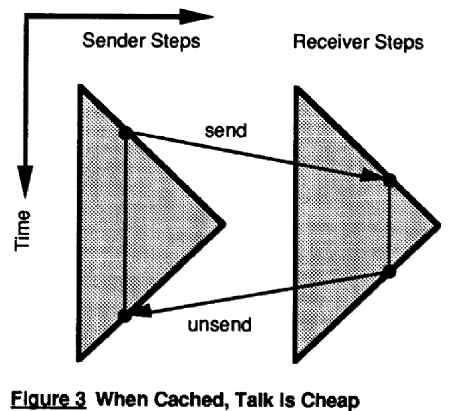
If the sender and recipient share enough synchronization to map their cycle ticks onto each other, and if messages can arrive by predictable deadlines, then messages can be unsent just when they are needed, and so any recording of the times of message arrival can be undone later, and need not waste bits. On the other hand, if clock drift is unpredictable, then of course it may cost a few bits to measure and correct for this.
First we need to define some terms. Let all the input, output, and extra registers hold S bits, and let the physical devices run at speeds so as to waste eS bits from friction per computing unit per cycle, for a total of 2neS bits per cycle.
The waste from from having a finite grand cycle should be qSk-n, where q is the average percentage remaining in a register after it has been compressed as much as possible relative to later registers. These two wastes can be designed to be about the same by choosing k-n/n ~ 2e/q. Let the measuring module collects fS bits of feature data each cycle, and let a percentage c of this change over a grand period. Thus cfS bits are wasted per cycle. If this waste is to be less than the previous two sources, then f <~ 2ne/c. This is a fairly strict constraint, and is likely to be a dominant one.
Perhaps even stricter are space constraints. The space to store the feature cache is fSkn on average, compared to ~knS for the basic reversible recursion. Thus if the feature cache is not to dominate space, one needs f <kn2e/q. The ratio of the two constraints on f is knc/q, so if kn is chosen high enough, then feature bit waste becomes the limiting factor, rather than cache storage. The storage cost of message caches is similarly ~ mSkn where mS is the average message bits per cycle, leading to a similar constraint on m.
[2] Bennett, C. (1989) "Time/Space Trade-Offs For Reversible Computation", SIAM J. Comput, V18, N4, August, pp. 766-776.
[3] Keyes, R. (1988) "Miniturization of electronics and its limits", IBM J. Res. Dev., V32 N1, Jan., pp. 24-28.
[4] Drexler, E. (1992) Nanosystems - Molecular Machinery, Manufacturing, and Computation, Wiley, NY.