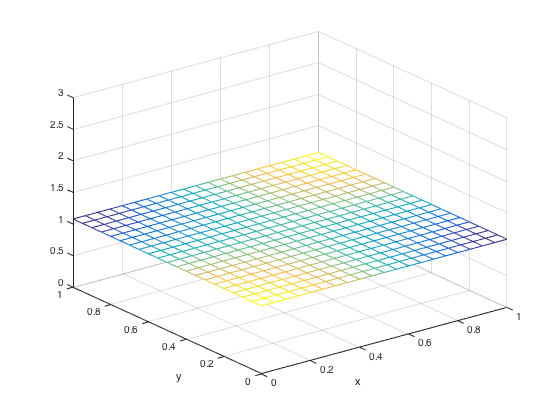
Example 8.14 dealt with solving Fisher's equation in 2 dimensions. The equation and boundary conditions used can be seen below: \[\begin{cases} u_t=D\Delta u +u(1-u) \\ u(x,y,0) = 2+cos(\pi x)cos(\pi y) \text{ for } 0 \geq x, y\leq 1\\ u_{n}(x,y,t) = 0 \text{ on rectangle boundary, for all } t \geq 0\end{cases}\] The code was provided from the text and can be seen here. The code solved Fisher's equation on a two-dimensional domain with Neumann boundary conditions, using a backward difference method with Newton's iteration. This code provided a final plot that showed the solution going toward the equilibrium solution of 1. The image of this can be seen below:
