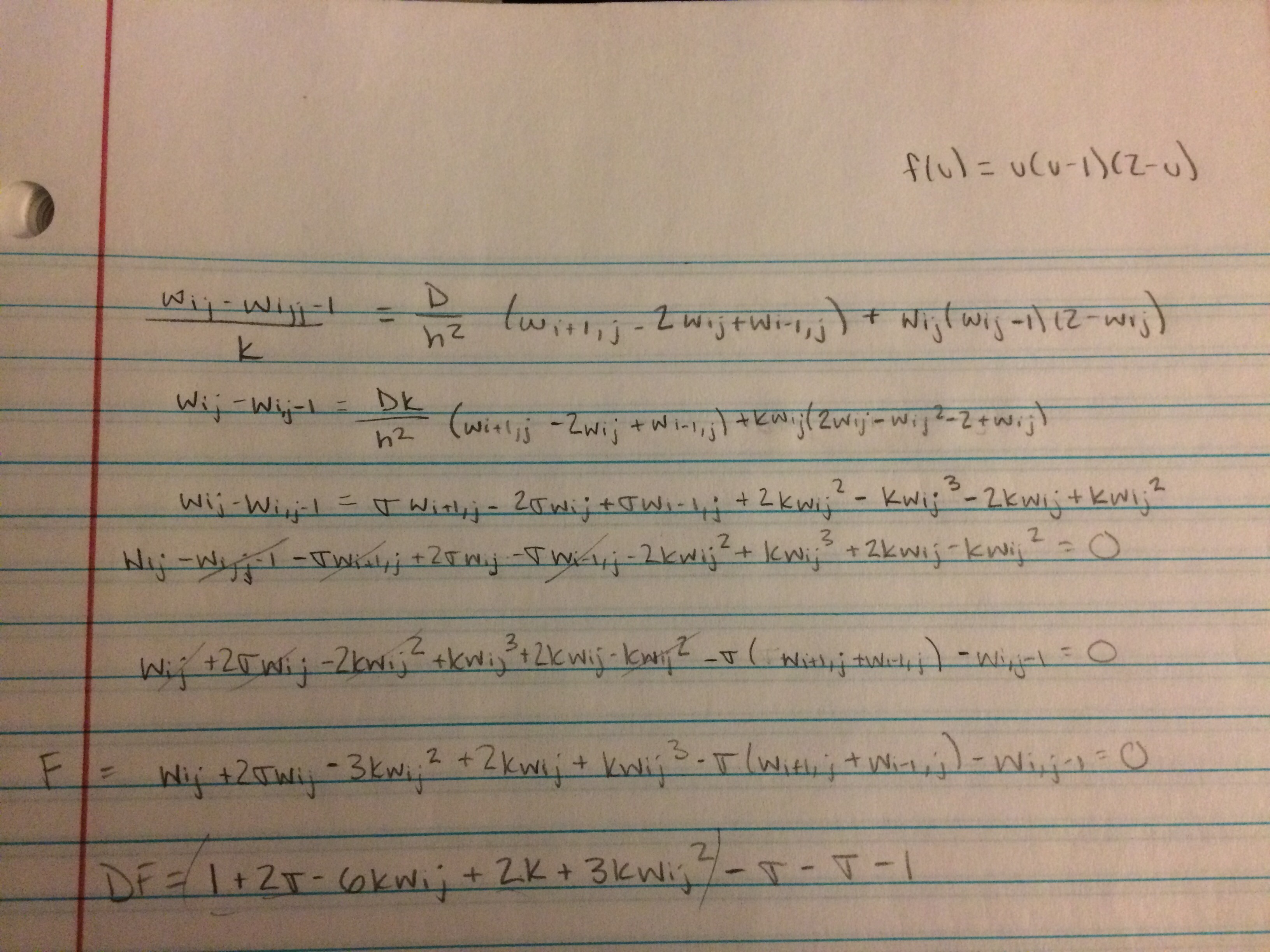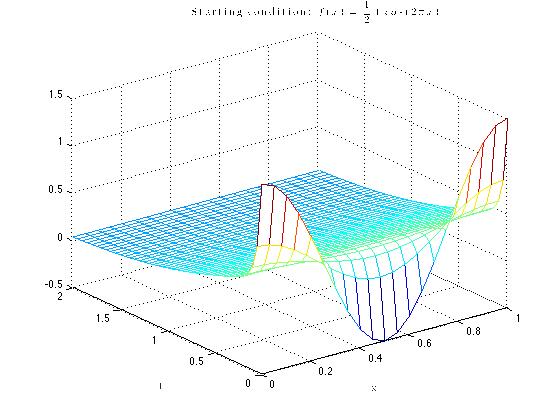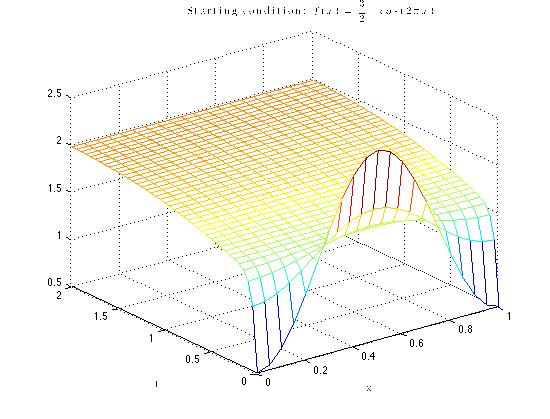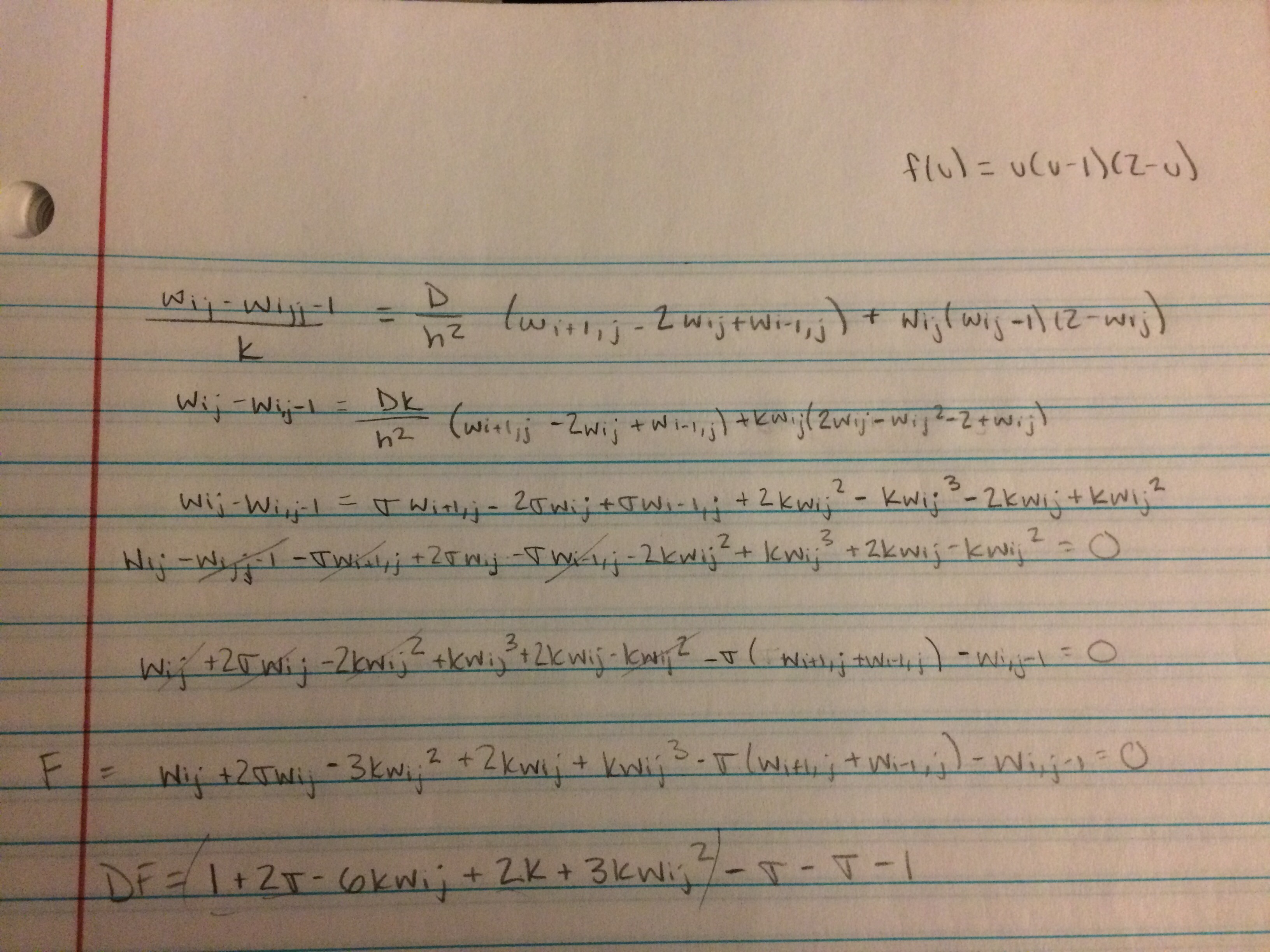
Exercise 8.4.4 and Computer Problem 8.4.3

Stephen Collins, Paul McNulty, Hannah Andrada, and Kathleen McLane

Exercise 8.4.4 dealt with finding the equilibrium points for \( f(u)=u(u-1)(2-u)\) and figuring out which ones were stable and which were unstable. By setting the function equal to zero, it was found that the equilibrium points were 0,1, and 2. To determine what values are stable and unstable, the derivative of the function was found, and the equilibrium points were plugged back into the equation. If the value is less than zero, than the point is stable. Doing this, it was found that 0 and 2 were stable, and 1 is unstable. This means that the solutions should go toward those values.

The next part of the project dealt with using the equilibrium points found, and \( f(u)=u(u-1)(2-u)\) to solve Fisher's equation. To do this, the code for Fisher's equation needed to be changed, such that the new \( f(u) \) could be used. To do this, the work was written up so that the correct matrix could be produced for the finite differences method. The work for this can be seen in the image below:

Using this work, the new code could be created, and seen here. From this code, two different initial conditions were used. The first was \( f(x) = 1/2 + cos(2\pi x) \) and the second was \( f(x) = 3/2 -cos(2 \pi x) \). Upon first look, it was expected that the solution would go toward 0 for the first initial condition, and go toward 2 for the second initial condition. Solution where the initial condition is \( f(x) = 1/2 + cos(2\pi x) \)

Solution where the initial condition is \( f(x) = 3/2 -cos(2 \pi x) \).

Home Part 1 Part 3