Whole Number Algorithms and a Bit of Algebra!
Using Base Ten Blocks to "See" Algorithms
Objective
To look at addition, subtraction, multiplication and division of whole numbers from a geometric, "hands-on" perspective and an algorithmic perspective.
Audience
This activity is intended for teachers. The activity is designed to make connections between the use of manipulatives and the development of algorithms. Parents and students are welcomed!
Materials Needed - Virtual Manipulative Base 10 Blocks!
Instructions
You may want to print this page for documentation.
- Open the virtual Base 10 Blocks.
- Click on the place value mat icon to change the background, if you need.
- Click on the figures to get the units, tens, and hundreds pieces.
- Click on the hammer, glue, or lasso to help do your work!
Developed by Jacobo Bulaevsky.
Operations

Part 1: Addition
- One Type of Addition Algorithm
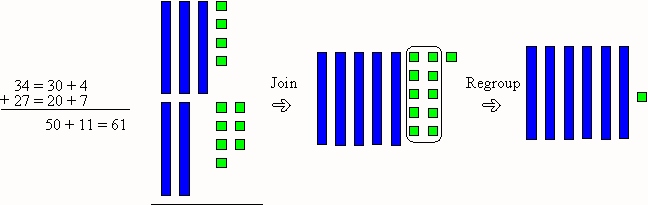
- Try these problems using Base 10 Blocks and the algorithm. Document your work.

Part 2: Subtraction
- One Type of Subtraction Algorithm
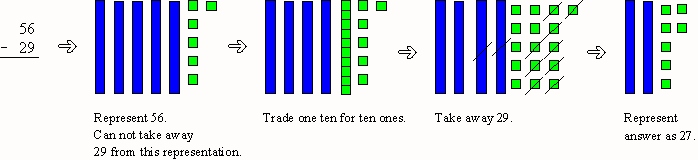
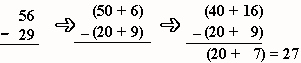
- Try these problems using Base 10 Blocks and the algorithm. Document your work.

Part 3: Multipication
- One Type of Multiplication Algorithm - If you have 23 students in your class and they each
need 12 straws for a craft project, how many straws do you need to supply? We write this as 23
groups of 12 or 23 × 12. Write out how you would find the solution to this problem.
- Notice two applications of the Distributive Property gives us the "standard" pieces. Here
you see this in both vertical and horizontal formats. Find the pieces from the computations below
on the area model. Notice that we are actually finding 12, 23's.
- Try these problems using Base 10 Blocks. Draw or printout the area model you construct. Write out the details of the algorithm and find the products
on your area model. Notice that the second problem is multi step. (Why?)

Part 4: Division
- One Type of Division Algorithm - You have 483 sea shells for a class art project. Each student needs 21 shells. How many
students will be able to make the project? How many groups of 21 shells can you form out of 483
objects? We write 483 ÷ 21. Write out how you would find the solution to this problem.
- Find the number of groups of size 21 are on the Area Model. Draw in the left most column with the
appropriate "Base 10 Blocks."
- Next, look at the scaffold method below. (Is there a correlation to the scaffold "good guess"
method and the Area Model? Does there have to be a relationship?)
| Scaffold:
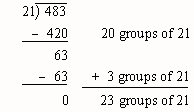 |
 |
- Now, you have 483 sea shells for a class art project. There are 21 students in your class. If
you give each student the same number of shells, how many shells will each student have? Use
the blocks to model this problem. Is it still written 483 ÷ 21? Discuss.
- Try these by drawing Base 10 Blocks. Then, write out the solution using the scaffold method.
Teacher Note: When you pick problems for illustration with Base 10 blocks, make sure you check
them out first using the blocks! Sometimes a problem requires that you break up a FLAT in order
to fill in the area model. This type of problem is not the best for a first use of the blocks.

Part 5: Moving to Algebra!
We can use the Base 10 blocks concept to create XY Blocks. X and Y are unknown lengths!
Optional: Click here to make a set of XY Blocks. Use the Back button to return to this page.
We will only need X Blocks for this activity.
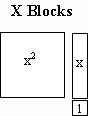
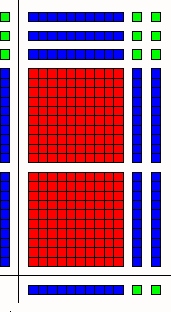
- Look at the figure below. This is an area representation of (x + 2)( x + 3). Compare this
to 23 ×12. Do you see a similarity?
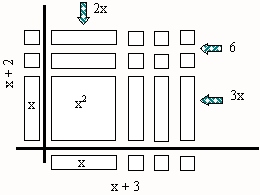
- Now expand (x + 2)(x + 3) using the distributive property: (x + 2)(x + 3) =
- Find each term of (x + 2)(x + 3) on the picture above.
- Try these! Draw them out and then expand. Can you see the terms on your area model?
- x(x + 4)
- (x + 1)(2x + 3)
- Extension: Draw and expand (x + 2y + 3)(2x + y). Hint: You will need a y and y2 block.
Top |
Use the Back button to return!
Copyright  1998 by
Margo Lynn Mankus
1998 by
Margo Lynn Mankus

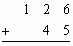


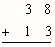
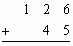


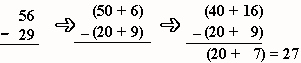
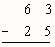


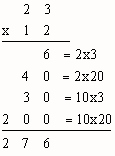
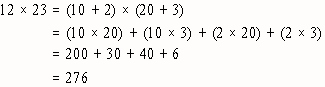
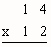
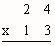

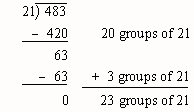

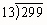
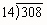



 1998 by
Margo Lynn Mankus
1998 by
Margo Lynn Mankus