Orthogonal Bases for Images, Coding, and Compression via Gabriel Peyrê

This section introduces Entropy Coding and Compression. In the words of Mr. Peryê, "Entropic coding converts a vector x into a binary stream y. Entropic coding exploits the redundancies in the statistical distribution of the entries of x to reduce as much as possible the size of y. The lower bound for the number of bits p of y is the Shannon bound p=-sum_i h(i)*log2(h(i)), where h(i) is the probability of apparition of symbol i in x." (1) To put this in simpler terms:

1. Take a vector or matrix, of values. For our interests, imagine a matrix containing values of an audio or image file.

2. Take a transform of one's liking. Be it DFT, DCT, Wavelets...etc.

3. Quantize the values of the matrix after the transform. Quantization will be discussed later, but consider it a strategic rounding for now.

4. This where the entropy coding comes in. This process of entropy coding takes the entire series of distinct quantized values in a signal, and based on the probability of the appearance of the distinct value, assigns a certain number of bits to represent that value. The formula for the total number of bits is:

Where k represents the number of distinct quantized values and represents the probability of the appearance of a value at any point. Through this process one can represent a value that appears more often with a fewer number of bits. For example, for the value that appears most frequently, one can represent that specific value with a "0." This takes only 1 bit. This idea leads us to the first type of entropy coding in the section.

With Huffman coding one seeks a means of compressing a set of values along the lines mentioned in the above paragraph. In the cases of images, Huffman Coding is a means of a further compression of values, such as Fourier or Wavelet coefficients. This gives people the means to send a picture using less bandwith. Once received, the recepient individual must decode the Huffman Coding, and then perform an inverse transform of some kind using the quantized coefficients they received. One of the hallmarks of Huffman Coding, is the Huffman Tree. One can generate the Huffman Tree in the following manner.

(1) Begin with the a set of probabilities. These represent the occurance of a value in your signal. These are generally quantized so any value is an integer of some kind. Some probabilities used by Mr. Peryê are given below:

The Huffman Tree shown below shows the resulting Huffman Coding of the values for the vector h.

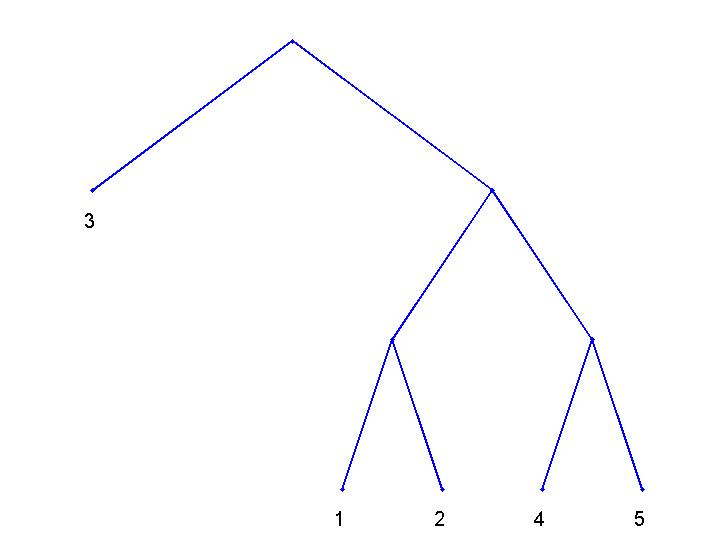
The Huffman Tree enables binary code to be read in order to reconstruct a signal of some kind. The construction of the Huffman Tree involves starting with the smallest two probabilites, combining them, and forming a branching of the tree. This process of combinations and branching is repeated until all the probabilities have been put into the tree. At each value in the tree, a binary value has been assigned. As we expect, the value of 3, which has the largest probability is 0. This makes sense, because we want the value most used in the signal reconstruction to be represented by the least number of bits. In the case of the signal used in this example, with probablities h, Huffman Coding works very well, and is only a slight bit above the Entropy bound. However, as will be shown in the preceeding section, Huffman Coding does not always work as well as we would like it to.

The first form of Huffman Coding that was investigated above runs into inefficiencies if one of the probabilities is very large. There is a way to get around this with Huffman Block Coding. One replaces their set of distinct symbols with different symbols. This breaks up the symbol with a large probability in smaller symbols. This is helpful in approaching the Shannon Entropy Bound. Mr. Peyrê proceeds to generate a distribution of 8 distinct signals from an initial signal "h", with the following probabilities:

This then turns into:

Adding blocks is helpful in approacing the Entropy Bound of the signal. Mr. Peryê demonstrates this by sucessfully adding more blocks to the signal.

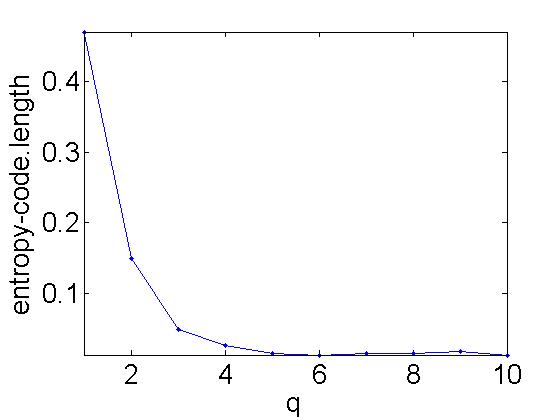
Entropy=0.52936. Huffman(block size 1)=1

Huffman(block size 2)=0.67578

Huffman(block size 3)=0.57703

Huffman(block size 4)=0.55188

Huffman(block size 5)=0.54358

Huffman(block size 6)=0.54224

Huffman(block size 7)=0.54956

Huffman(block size 8)=0.54443

Huffman(block size 9)=0.5481

Huffman(block size 10)=0.54224

As one can see, adding more and more blocks is beneficial in reaching the Shannon Entropy Bound. In the words of Mr. Peyrê, "A block coder is able to reach the Shannon bound, but requires the use of many symbols, thus making the coding process slow and memory intensive." (2) The next section offers an improvement on the two previous coding methods that were investigated.

In the words of Mr. Peyrê, the Arithmetic Coding "encodes a stream using an interval." (3) The function that Mr. Peyrê writes for Arithmetic Coding is a bit complicated, and requires both coding and decoding. The histogram below crudely shows the random signal used in this example.

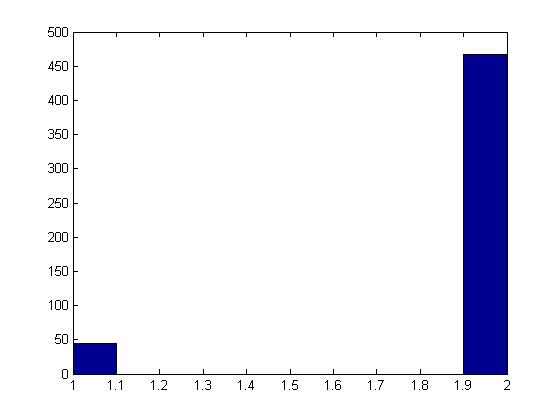
He then uses his arithmetic coding function to code the signal and then compares it to the Shannon Entropy Bound: Entropy=0.469, arithmetic=0.467.

The function he wrote is very complicated and at this time, I am choosing not to investigate it thoroughly. Should I choose to study Entropy Coding in the future, I will definitely have to invest more time into this function.

In my studies of audio compression in the spring, I did a brief study of Huffman Coding. This section has shown me an improved form of Huffman Coding, as well as a rather complicated alternative to it. Seeing how Mr. Peyrê generated the Huffman Tree is very useful and taught me a lot. I am going to skip the Natural Images Statistics section and proceed to the Image Compresison with Wavelets section.

• Home
• Image Compression with Wavelets

Works Cited

(1) Peryê, Gabriel. "Entropic Coding and Compression." Entropic Coding and Compression. N.p., 2008. Web. 21 July 2014. .

(2) Peryê, Gabriel. "Entropic Coding and Compression." Entropic Coding and Compression. N.p., 2008. Web. 25 July 2014. .

(3) Peryê, Gabriel. "Entropic Coding and Compression." Entropic Coding and Compression. N.p., 2008. Web. 25 July 2014. .

G. Peyré, The Numerical Tours of Signal Processing - Advanced Computational Signal and Image Processing, IEEE Computing in Science and Engineering, vol. 13(4), pp. 94-97, 2011.