Part X: Image Compression with Wavelets

This section involves the method of quantization. Quantization is means of "calculated rounding." After one takes a transform of their liking, be it Fourier, Wavelet, Cosine, etc, they can then quantize their coefficients. From here, one can proceed much more easily to Entropy Coding. In this section, with the help of Mr. Peyrê, I will be quantizing Wavelet coefficients. First, Mr. Peyrê creates an vector of 2048 values and with the help of the floor and sign function, creates an evenly distributed vector with integer values. It is shown on the left, in the plot below.

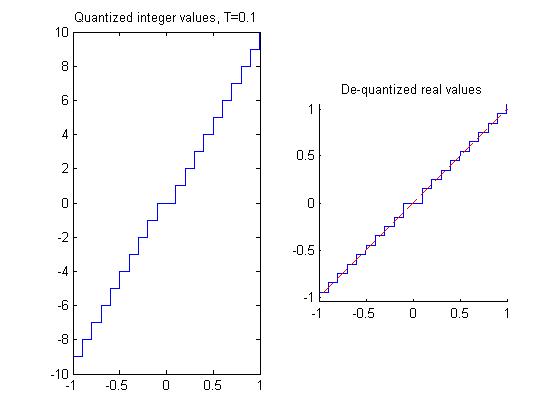
After the quantization part, a de-quantizatiion is performed. This represents an attempt to "de-round" or recover the original values from the quantized values. In this example, not all of the original values in the first vector are recovered, but it is very close nevertheless. The graph on the right, plots the original vector in red, and the de-quantized values in blue. Notice that the original vector is linear, while the de-quantized approximation has several discontinuities.

Now we get to the fun stuff. This example will feature a non-linear Wavelet approximation with quantization. This means that not only will Wavelet coefficients below a certain threshold be set to zero, but those above that threshold will be rounded from quantization. The plot below shows the the thresholded coefficients, followed by the quantized thresholded coefficients.

Next, Mr. Peyrê uses a thresholding and quantizing value of .2. A larger quantizing value yields a stronger compression.

The resulting image is quite good. The high details elements of the image still remain intact without being overly diminished. The overall size of the file has been reduced by 1 KB. Mr. Peyrê next proceeds to implement a spatial quantization in an attempt to match the previous approximation. This means he is doing the quantization in the spatial domain, i.e., no transforms of the image are being performed. The result of this process is given below>

Not only does this spatial compression look bad, it results in a larger file size than the original. This is really quite odd. Suffice to say, I am not overly impressed with spatial domain quantization.

Now, we make use of the Entropy Coding discussed in the previous section, to add a further degree of compression to the image. As Mr. Peyrê says, "To reduce the number of bits, an entropic coder makes use of the statistical distribution of the quantized values." (1) Mr. Peyrê first proceeds to quantize and de-quantize the Wavelet coefficients. After that, he quantizes the pixel values of the original image. Below are two different histograms. The top histogram shows the distribution of the quantized pixel values. The histogram on the bottom shows the quantized Wavelet coefficients.

Next, Mr. Peyrê compares the entropy between the quantized pixels and the quantized Wavelet coefficients. As one might guess, the entropy in the Wavelet coefficients is less than the entropy in the pixel values. This is because many of the Wavelet coefficients are set to 0 in the quantization process. The results are given below:

Pixels entropy: 3.2

Wavelet entropy: 0.72

Mr. Peyrê closes this section with a very nice graph that shows the relationship between the number of bits per pixel of the Wavelet coefficients, and the quality of the image approximation. Using various compression rates, ranging from 0.03 to 0.6, Mr. Peyrê performs quantization of the Wavelet coefficients and then computes the resulting SNR of the approximation. A smaller value of compression gives more bit per pixel, and yields a better approximation to the image. The number of bits is determined by the entropy in the quantized Wavelet coefficients.

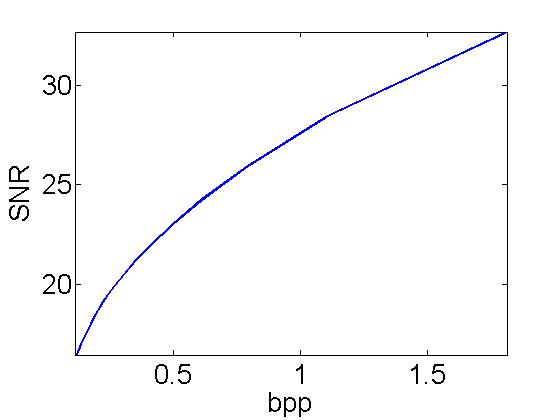
One sees a roughly linear error rate from 1.5 to 1, from 1 on down, the error rate begins to pick up though. This relationship is very interesting. One does not usually want their SNR to fall below 25 or so, from my experience so far.

As it turns out, one can add a further degree of compression to their image by taking the Wavelet coefficients in different directions, namely horizontal, vertical, and diagonal. This is done because the Wavelet coefficients in different directions have varying degrees of entropy. This is proven in the first part of the section:

Entropy, all: 0.287

Entropy, horizontal: 0.466

Entropy, vertical: 0.212

Entropy, diagonal: 0.157

Next he shows how many bits per pixel are needed in two cases - the first using no directional seperation of the Wavelet coefficients, and the second, using the directional seperation.

nb.bis, whole: 0.719 bpp

nb.bis, separate: 0.58 bpp

This shows that if one uses a directional seperation of the Wavelet coeffcients, the resulting compression is more efficient. This results because "The Wavelet coefficients of an image do not have the same distribution across the scales." (2) The plot below shows a comparison between vanilla Wavelet compression, and directional Wavelet compression. Its a very nice result.

What does this tell us? It says that if we seperate the Wavelet coefficients, we can get away with a higher degree of compression, relative to "vanilla" Wavelet compression. In other words, given a certain compression rate, the seperated Wavelet coefficients will have a higher SNR. It goes without saying that one should seperate their Wavelet coefficients should they want to compress their image.

This section was a fun look at Wavelet compression. It built upon the Entropy Coding that I studied in the previous section. I had previously studied quantization of digital audio in my Audio Codec project (see the Math 447 projects of my website), so I had some familiarity with the idea of quantization. My favorite part of this section was the directional seperation of the Wavelet coefficients. Its pretty awesome! My study of Wavelets continues to be novel and exciting. In the next section, I look at Wavelet Domain Watermarking.

Works Cited

(1) Peryê, Gabriel. "Image Compression with Wavelets." Image Compression with Wavelets. N.p., 2008. Web. 01 Aug. 2014. .

(2) Peryê, Gabriel. "Image Compression with Wavelets." Image Compression with Wavelets. N.p., 2008. Web. 04 Aug. 2014. .

G. Peyré, The Numerical Tours of Signal Processing - Advanced Computational Signal and Image Processing, IEEE Computing in Science and Engineering, vol. 13(4), pp. 94-97, 2011.