|
|
George Mason University
Conor Philip Nelson
Source: Home > Classes > Math 447 > Project 5 > Step 1
Math 447: Numerical Analysis
Computer Problem 11.2.3
3. Obtain a grayscale image file of your choice, and use the \(imread\) command to import into Matlab. Crop the resulting matrix so that each dimension is a multiple of 8. If necessary, converting a color RGB image to gray scale can be accomplished by the standard formula (11.15).
(a) Extract an 8×8 pixel block, for example, by using the Matlab command \(xb=x(81:88,81:88)\). Display the block with the imagesc command.
(b) Apply the 2D-DCT.
(c) Quantize by using linear quantization with \(p=1,2\) and \(4\). Print out each YQ
(d) Reconstruct the block by using the inverse 2D-DCT, and compare with the original. Use Matlab commands \(colormap(gray)\) and \(imagesc(X,[0 255])\).
(e) Carry out (a)–(d) for all 8×8 blocks, and reconstitute the image in each case.
Please note that entire problem utilizes ChangeToGray.m and ReconstrcutGray.mS
[(a)-(d)] I used \(xb=x(200:207,200:207)\). This is close to the center of the image
|
\(p=1\)
\[
\left(
\begin{matrix}
-13 & -7 & 0 & 1 & 0 & 0 & 0 & 1\\
-1 & 0 & -1 & 0 & 0 & 0 & 0 & 0\\
2 & 1 & 0 & 0 & 0 & 0 & 0 & 0\\
1 & 0 & 0 & 1 & & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
\right)
\]
|
\(p=1\) 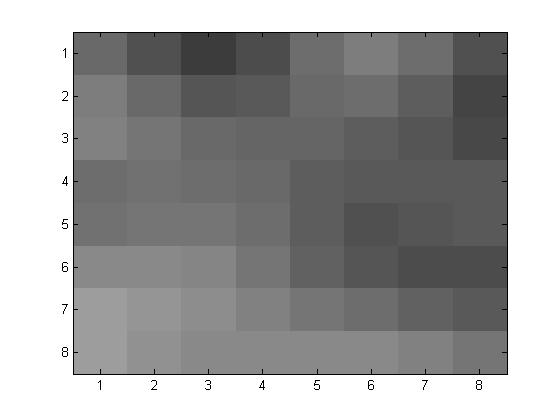
|
Original 
|
|
\(p=2\)
\[
\left(
\begin{matrix}
-6 & -3 & 0 & 1 & 0 & 0 & 0 & 0\\
0 & 0 & -1 & 0 & 0 & 0 & 0 & 0\\
1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
\right)
\]
|
\(p=2\) 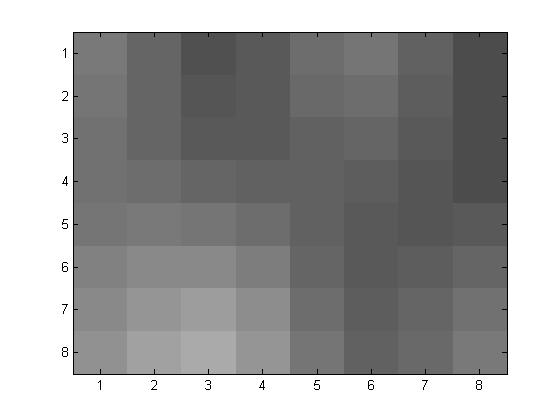
|
Original 
|
|
\(p=4\)
\[
\left(
\begin{matrix}
-3 & -2 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
\right)
\]
|
\(p=4\) 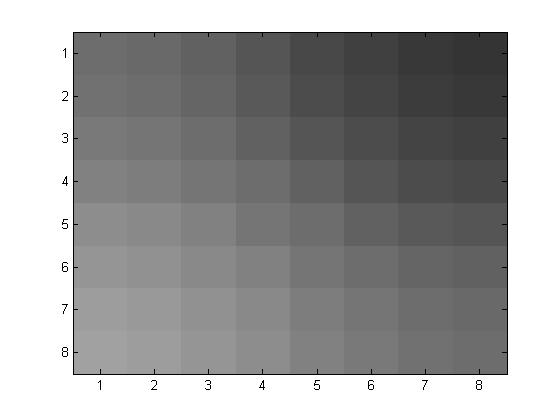
|
Original 
|
|
\(p=10\)
\[
\left(
\begin{matrix}
-1 & -1 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
\right)
\]
|
\(p=10\) 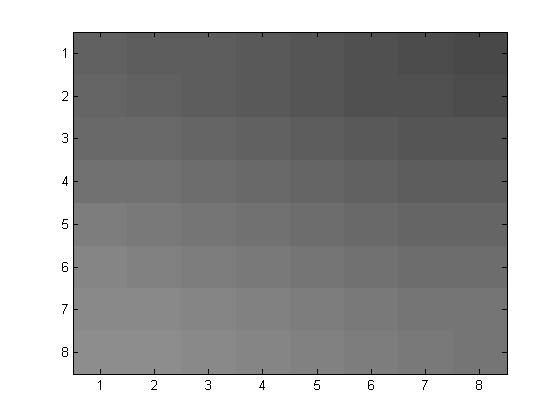
|
Original 
|
|
\(p=14\)
\[
\left(
\begin{matrix}
-1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\
0 & 0 & 0 & 0 & 0 & 0 & 0 & 0
\end{matrix}
\right)
\]
|
\(p=14\) 
|
Original 
|
After using reconstruct gray:
(e) Finally, we will pull together all 8x8 blocks.
\(p=1\) 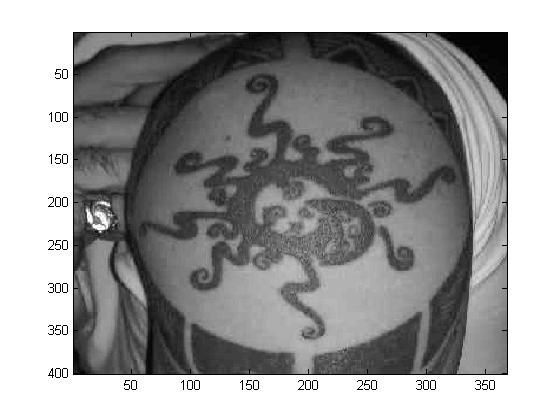
|
Original 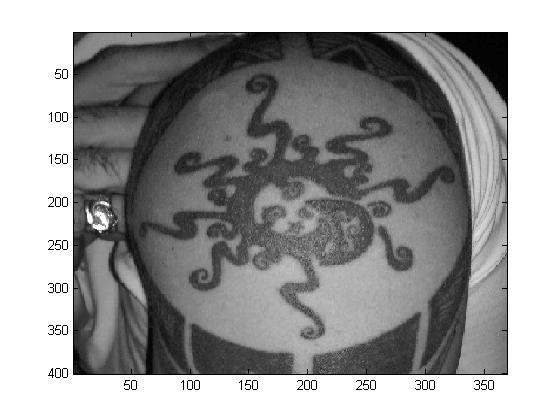
|
\(p=2\) 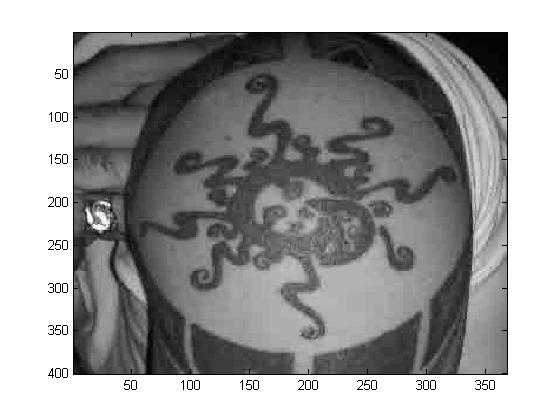
|
Original 
|
\(p=4\) 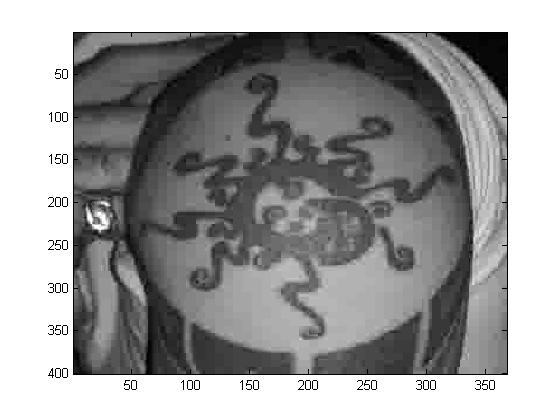
|
Original 
|
\(p=10\) 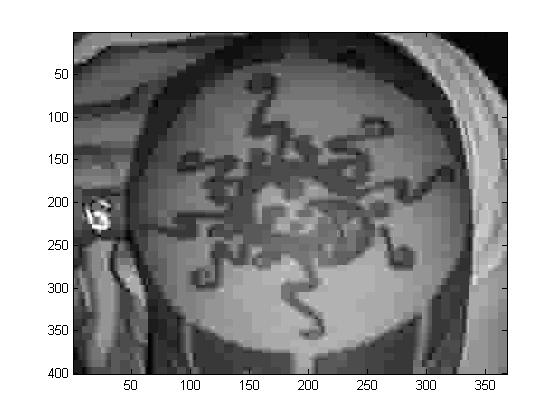
|
Original 
|
\(p=14\) 
|
Original 
|
|


