George Mason University

Conor Philip Nelson

A remarkable three-body figure-eight orbit was discovered by C. Moore in 1993. In this configuration, three bodies of equal mass chase one another along a single figure-eight loop. Set the masses:
\(m_1=m_2=m_3=1\) and gravity \(g=1\)

(a) Adapt \(orbit.m\) to plot the trajectory with initial conditions:
\((x_1,y_1)=(-0.970,0.243)\) . \((x_1',y_1')=(-0.466,-0.433)\)
\((x_2,y_2)=(-x_1,-y_1)\) . \((x_2',y_2')=(x_1',y_1')\)
\((x_3,y_3)=(0,0)\) . \((x_3',y_3')=(-2x_1',-2y_1')\).

(b) Are the trajectories sensitive to small changes in initial conditions? Investigate the effect of changing \(x_3'\) by \(10^{-k}\) for \(1 \leq k \leq 5\). For each \(k\), decide whether the figure-eight pattern persists, or a catastrophic change eventually occurs.

(a)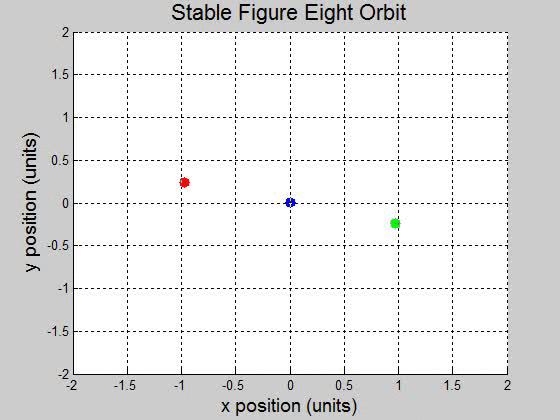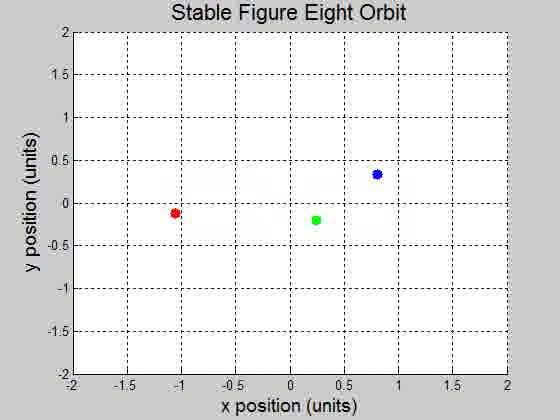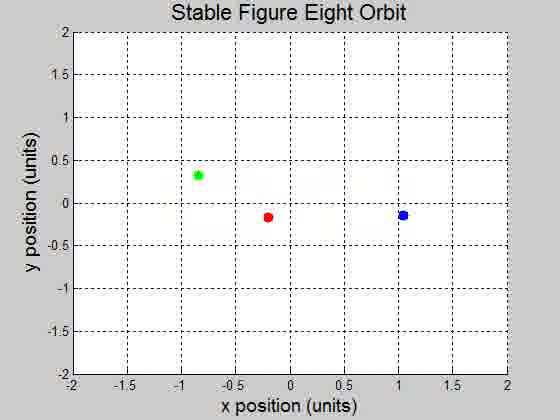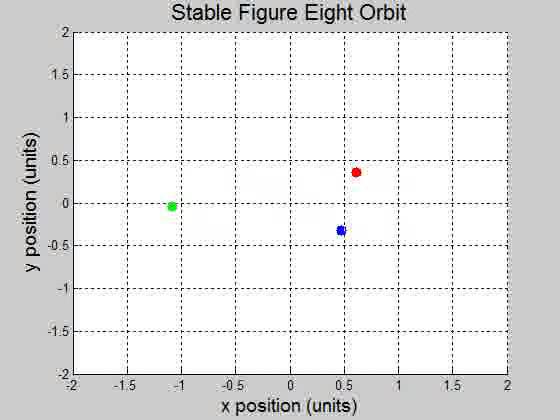



(b) For the interval [0 100] with 10000 steps, it surprisingly worked fine for \(10^{-2}\) and less. It caused the orbit to drift to the +x direction, but it didn’t break up the orbit. This might be a little difficult to show though, because it drifts way out.

\(k=1\)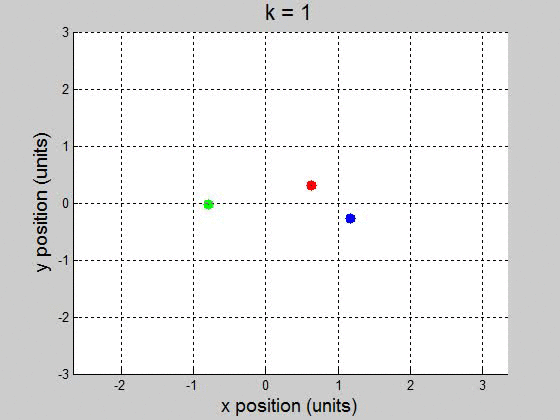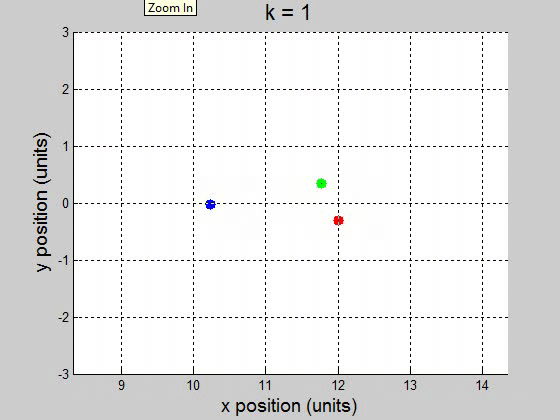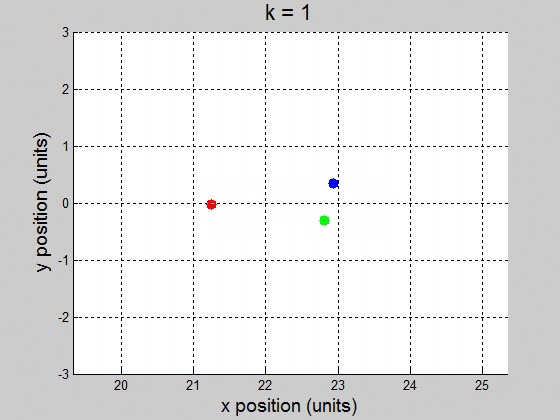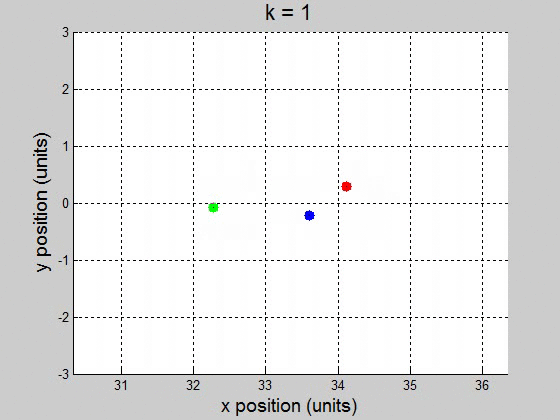


\(k=2\)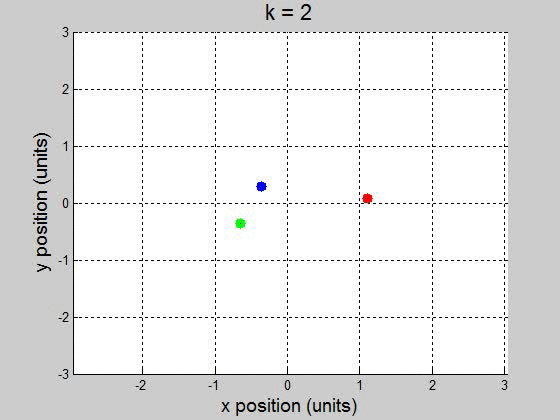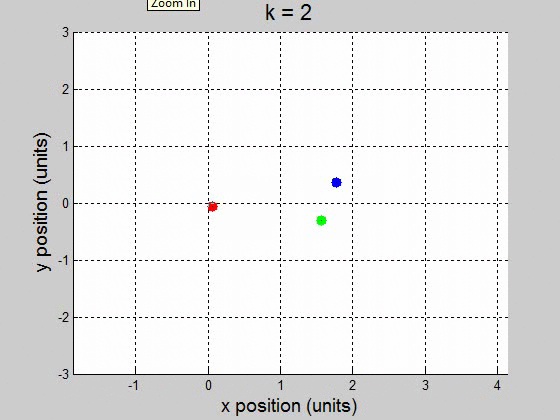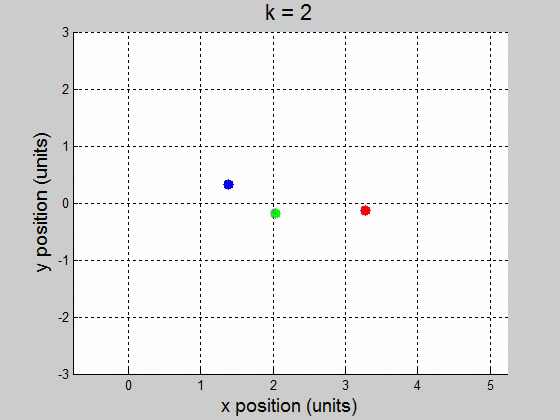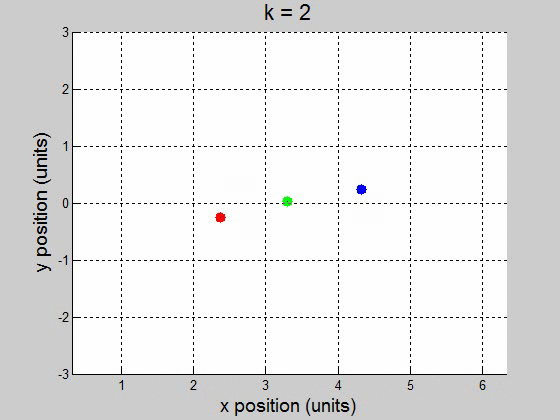


\(k=3\)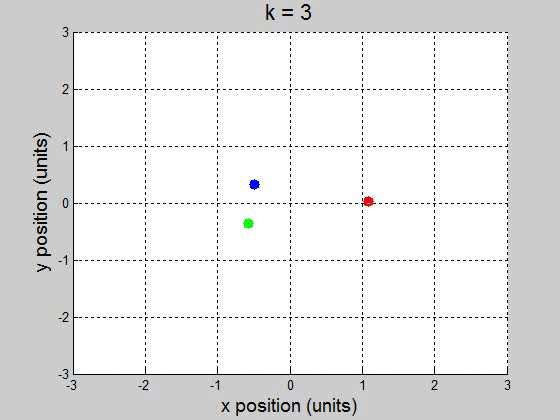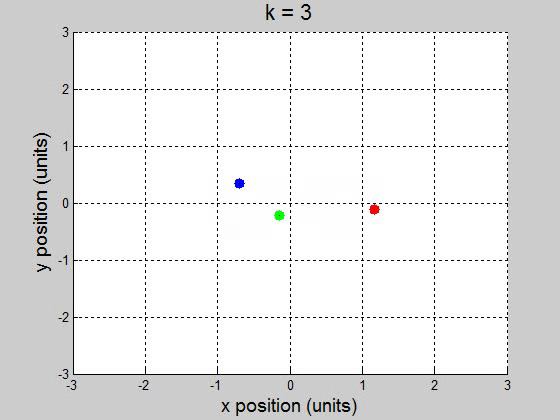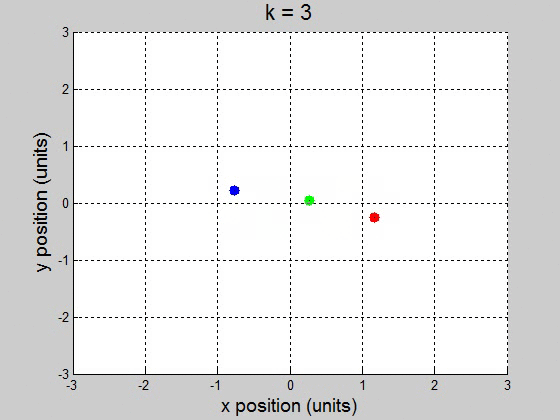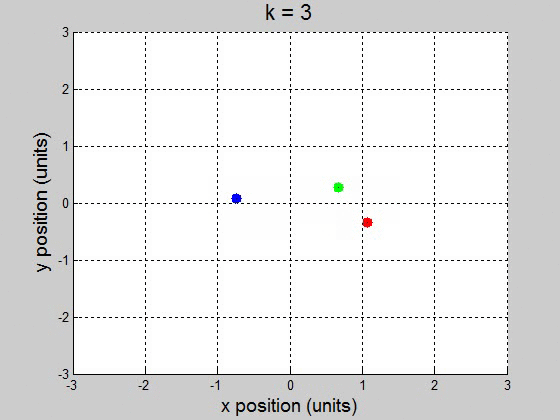


\(k=4\)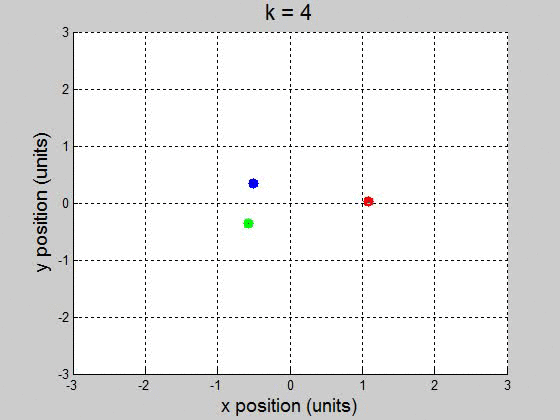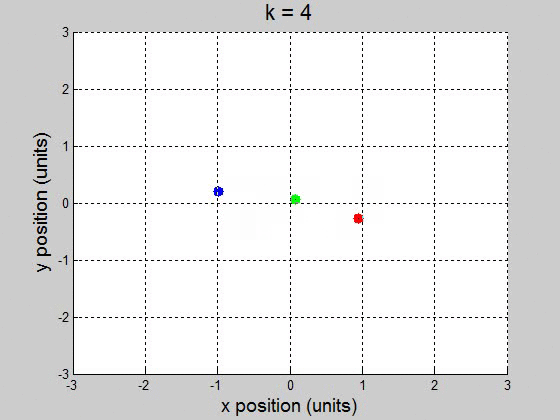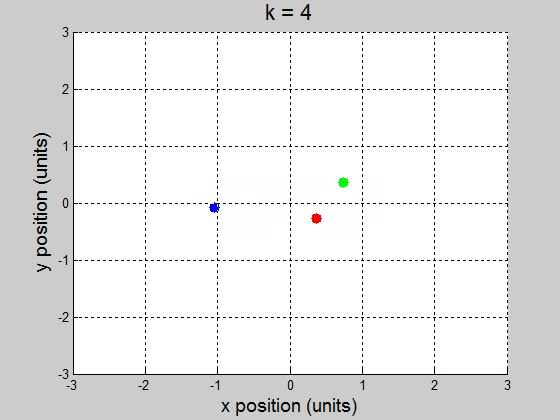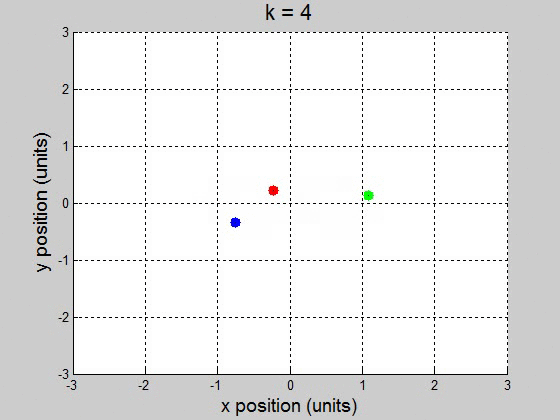

Previous: 6.3.10

Project 3 Home

Next: Extra Results