|
|
George Mason UniversityConor Philip NelsonSource: Home > Classes > Math 400 > Final Project > ApplicationMath 400: History of MathematicsConsider the definition of \(\Gamma(n)\): $$\Gamma(n)=\int^{\infty}_0e^{-x}x^{n-1}dx$$ Integrating by parts yields: $$\int^{\infty}_0e^{-x}x^ndx=-x^ne^{-x}|^{\infty}_0+n\int^{\infty}_0x^{n-1}e^{-1}dx=n\int^{\infty}_0x^{n-1}e^{-x}dx$$ Now $$\int^{\infty}_{0}e^{-x}x^{n}dx$$ is an integral of the same type as original, where \(n\) is replaced by \(n+1\). Thus $$\Gamma(n+1)=n\Gamma(n)$$ From this, consider when \(n=1\): $$\Gamma(1)=\int^{\infty}_0e^{-x}x^{1-1}=\int^{\infty}_0e^{-x}=1$$ Consider now then \(n=2,3,4...\), this follows: $$\Gamma(2)=1\Gamma(1)=1!$$ $$\Gamma(3)=2\Gamma(2)=2*1=2!$$ $$\Gamma(4)=3\Gamma(3)=3*2*1=3!$$ $$\vdots$$ $$\Gamma(n)=(n-1)\Gamma(n-1)=(n-1)!$$ $$\Gamma(n+1)=n\Gamma(n)=n!$$ We now know that this is defined for all integers \(n>0\). But what of \(n\leq 0\)? Consider this approximation: $$\lim_{n\rightarrow 0} \Gamma(n)=\frac{\Gamma(n+1)}{n}$$ $$\Gamma(0)=\infty$$ it follows that: $$\Gamma(-1)=\frac{\Gamma(0)}{-1}=\infty$$ $$\Gamma(-2)=\frac{\Gamma(1)}{-2}=\infty$$ and that \(\Gamma(-n)\) is infinite when \(n\) is positive integer. We wish to extend this concept to non-integer values. Consider \(\frac{1}{2}!\) $$\frac{1}{2}!=\Gamma(\frac{3}{2})=\int^{\infty}_0e^{-x}x^{\frac{1}{2}}dx$$ If the variable in this integral be changed by the transformation \(x=y^2\), the integral becomes $$\frac{1}{2}!=2\int^{\infty}_0e^{-y^2}y^2dy \dots (1)$$ Since the definite integral is independent of integration and is a function of limits, $$\frac{1}{2}!=2\int^{\infty}_0e^{-z^2}z^2dz \dots (2)$$ Consider multiplying (1) and (2), this yields: $$\left(\frac{1}{2}!\right)^2=4\int^{\infty}_0e^{-z^2}z^2dz\int^{\infty}_0e^{-y^2}y^2dy$$ which can be written as a double integral $$\left(\frac{1}{2}!\right)^2=4\int^{\infty}_0 \int^{\infty}_0 e^{-(y^2+z^2)}z^2y^2dydz$$ Consider now converting to polar coordinates, \(z=r\cos(\theta)\) and \(y=r\sin(\theta)\). Note also that \(dydz=rdrd\theta\). We have: $$\left(\frac{1}{2}!\right)^2=4\int^{\infty}_0dr\int^{\frac{\pi}{2}}_0r^5e^{-r^2}sin^2(\theta)cos^2(\theta)d\theta$$ "When the smoke clears:" $$\int^{\frac{\pi}{2}}_0 sin^2(\theta) cos^2(\theta) \theta d\theta=\frac{\pi}{16}$$ $$\int^{\infty}_0e^{-r^2}r^5dr=1$$ Therefore, $$\left(\frac{1}{2}!\right)^2=\frac{\pi}{4} \rightarrow \frac{1}{2}! =\frac{\sqrt{\pi}}{2}$$ Here we can see the graph of the function for values of negative and positive \(n\) 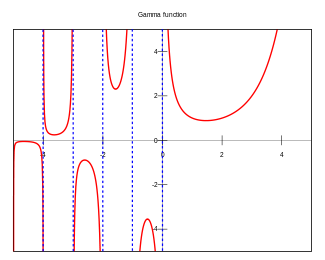
|