The work on this page was done by Anna-Rose Wolff, Chris Mazzullo, Shamaila Malik.
Consider a theoretical pendulum hanging from a rigid rod that is free to swing through 360 degrees. Using Newton's second law of motion, an equation to describe the motion of the pendulum can be found. The motion of the pendulum is constrained to a circle of radius l, where l is the length of the pendulum rod. Then if y is the angle of the pendulum with respect to the vertical in radians, ly'' is the component of acceleration tangent to the circle. The component of force along the direction of motion is mgsiny where m is the mass of the pendulum. Thus the differential equation governing the frictionless pendulum is mly'' = F = -mgsiny. This is a second order differential equation for the angle y of the pendulum. The initial conditions are given by the initial angle y(0) and angular velocity y'(0). This second order equation can be converted to the first-order system \[ \begin{align} y_1' = y_2 \\ y_2' = -\frac{g}{l} \sin y_1 \end{align} \] The code pend.m written by Doctor Sauer solves these equations numerically using the trapezoidal method.
The force of damping, such as air resistance or friction, is often modeled as being proportional and in the opposite direction to velocity. \[ \begin{align} y_1' = y_2 \\ y_2' = -\frac{g}{l} \sin y_1 - dy_2 \end{align} \] where \(d > 0 \) is the damping coefficient. By adding a damping coefficient, the pendulum will lose energy and over time approach the limiting equilibrium solution \(y_1 = y_2 = 0 \). To get more interesting behavior out of the pendulum, a time-dependent term representing outside forcing is added to the damped pendulum. \[ \begin{align} y_1' = y_2 \\ y_2' = -\frac{g}{l} \sin y_1 - dy_2 + A \sin t \end{align} \] The code for the forced, damped pendulum can be found here. By setting A equal to 0, the code above will model the damped pendulum.
A forced, damped pendulum with a high enough forcing parameter behaves chaotically. With a damping factor of 1, a forcing parameter A = 10 and a step size of .005 seconds, the pendulum moves like this:
| A damped pendulum modeled using trapeziod method and a step size of .005 seconds. |
However, with the same initial conditions and a higher step size of .01 seconds, the pendulum moves in a somewhat different way:
| A pendulum modeled using trapezoid method and a step size of .01 |
The forced, damped pendulum will move in particular patterns after a while, no matter what initial conditions it starts out with. These patterns of motion are called chaotic attractors because of how a pendulum's trajectory is drawn to them. With a damping factor of 1, a forcing parameter A = 10, and initial conditions y = \( \pi/2 \) and y' = 0, the pendulum settles into a pattern of three clockwise rotations followed by two counterclockwise rotations:
| This forced, damped pendulum's motion shows a chaotic attractor of three clockwise turns followed by two counterclockwise turns. |
Initial conditions of y = \( -\pi/2 \) and y' = 0 cause the pendulum to perform three counterclockwise rotations and two clockwise rotations, the mirror image of the other chaotic attractor:
| Notice that this pendulum performs three counterclockwise turns and two clockwise turns. This is a mirror image of the chaotic attractor shown in video 5-1. |
The pendulum's behavior changes radically when its pivot is made to oscillate. The differential equation describing the angle is: \(y'' + dy' + [\frac{g}{l} + A \cos 2 \pi t ] \sin y = 0 \) where A is the amplitude of the forcing function rotating the pivot. For high enough values of A, the two equilibrium points switch places. The stable equilibrium point at y = 0 becomes unstable, and the unstable equilibrium point at y = \( \pi \) becomes stable. To find the magnitude of the forcing function that causes this behavior, we first modeled the pendulum using a system of differential equations. By setting y equal to \( y_1 \) and y' equal to \( y_2 \), the system can be expressed as: \[ \begin{align} y_2' = -d * y_2 - [\frac{g}{l} + A \cos 2 \pi t ] \sin y_1\\ y_1' = y2 \end{align} \] A differential equation solver can approximate the pendulum's angle over time, and the pendulum's position can be plotted using the results. We found that the equilibrium point at y = \( \pi \) becomes stable for values of A between 19 and 25. Values of A higher than 25 cause the pendulum to oscillate faster and faster, eventually swinging around the bottom and orbiting around the pivot.
| With a forcing function of amplitude A = 25, the pendulum has a stable equilibrium at y = \( \pi \)! |
A pendulum with an oscillating pivot has an unstable equilibrium at y = 0 for some values of A. Using the model from the previous problem, we found that values of A greater than 15 made the equilibrium point at the bottom of the pendulum become unstable.
| With a forcing function of amplitude A = 15, the pendulum's formerly stable equilibrium at the bottom of its rotation becomes unstable! |
In step 8 we were asked to adadpt our pendulum program to build the double pendulum. The double pendulum is composed of a simple pendulum, with another simple pendulum hanging from its bob. From pend.m we created doublePend.m by first adding adding a new bob and rod (bob2, rod2), where the pivot end of the new rod is equal to the formerly free end of the first rod. The (x,y) position of the free end of the second rod was calculated using simple trigonometry. Setting \( y_1 \) and \( y_3 \) as the angles of the two bobs with respect to the vertical, the subprogram containg the right-hand side of our differential equations was updated with the following equations:
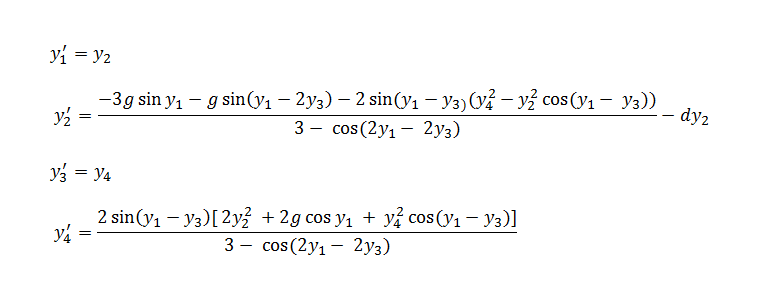
| This undamped double pendulum exhibits chaotic motion. |