Project 1: Kinematics of the Stewart Platform

Group Member: Aidan Curran and Varis Nijat

Question One
Question Two
Question Three
Question Four
Question Five
Question Six

A Stewart platform consists of six variable length struts, or prismatic joints, supporting a payload. Prismatic joints operate by changing the length of the strut, usually pneumatically or hydraulically. As a six-degree-of-freedom robot, the Stewart platform can be placed at any point and inclination in three-dimensional space that is within its reach

More Background Information

Our Goal is to solve the forward problem, namely, to find x,y,theta,given p1,p2,and p3

Question One

Write a Matlab function file for f (theta). The parameters L1,L2,L3,gamma, x1, x2, y2 are fixed constants, and the strut lengths p1,p2,p3 will be known for a given pose To test our code, substitute theta = -pi/4 or theta = pi/4, and we should get f(theta)=0

First Function

theta=pi/4;
result_1=f(theta)
theta=-pi/4;
result_2=f(theta)

result_1 =

  -4.5475e-13


result_2 =

  -4.5475e-13

Question Two

Plot f (theta) on [ -pi ,pi ]. Theree should be roots at +-pi/4

ezplot(@f,[-pi,pi])
hold on
plot([-pi,pi],[0,0])
hold off

Warning: Function failed to evaluate on array inputs; vectorizing the function
may speed up its evaluation and avoid the need to loop over array elements.

Question Three

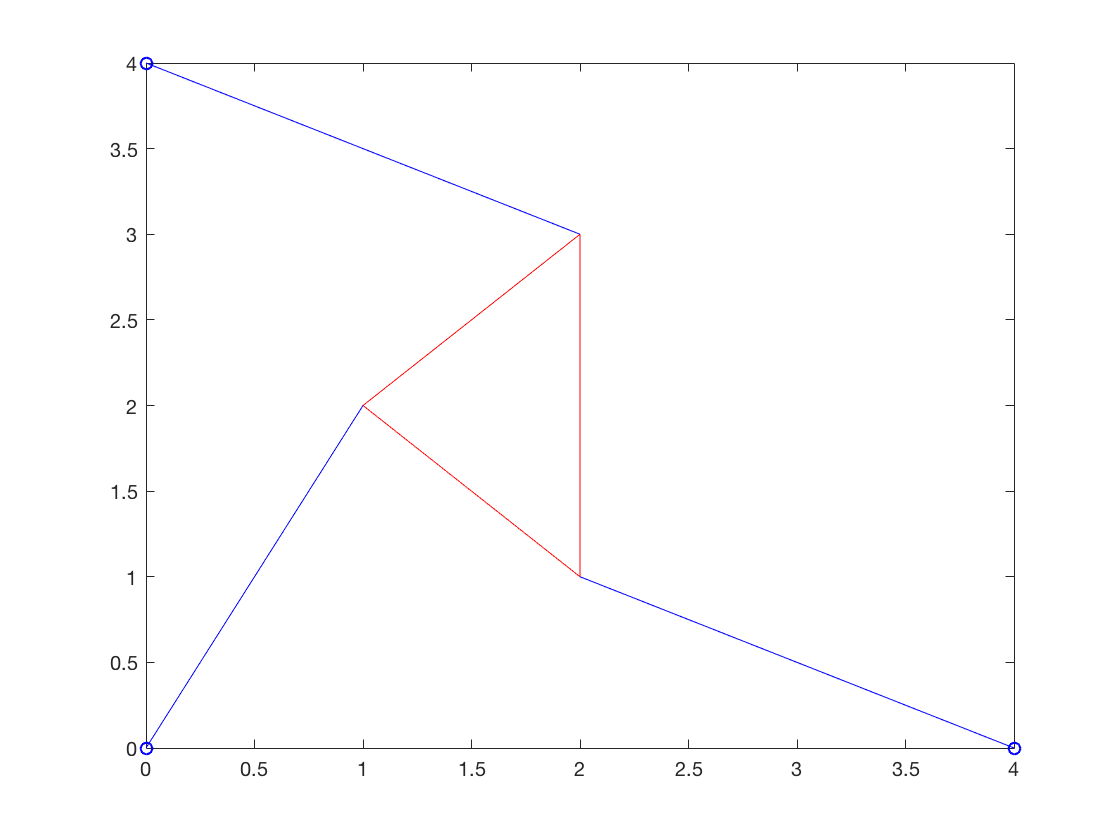
Reproduce Figure 1.15.

First Graph

x=1;y=2;
x1=4;
x2=0;y2=4;

u1=1;
u2=2;
u3=2;

v1=2;
v2=1;
v3=3;

plot([u1,u2,u3,u1],[v1,v2,v3,v1],'r');
hold on
plot([0,x1,x2],[0,0,y2],'bo')

plot([0 1],[0 2],'b')
plot([0,2],[4,3],'b')
plot([4 2],[0 1],'b')
hold off

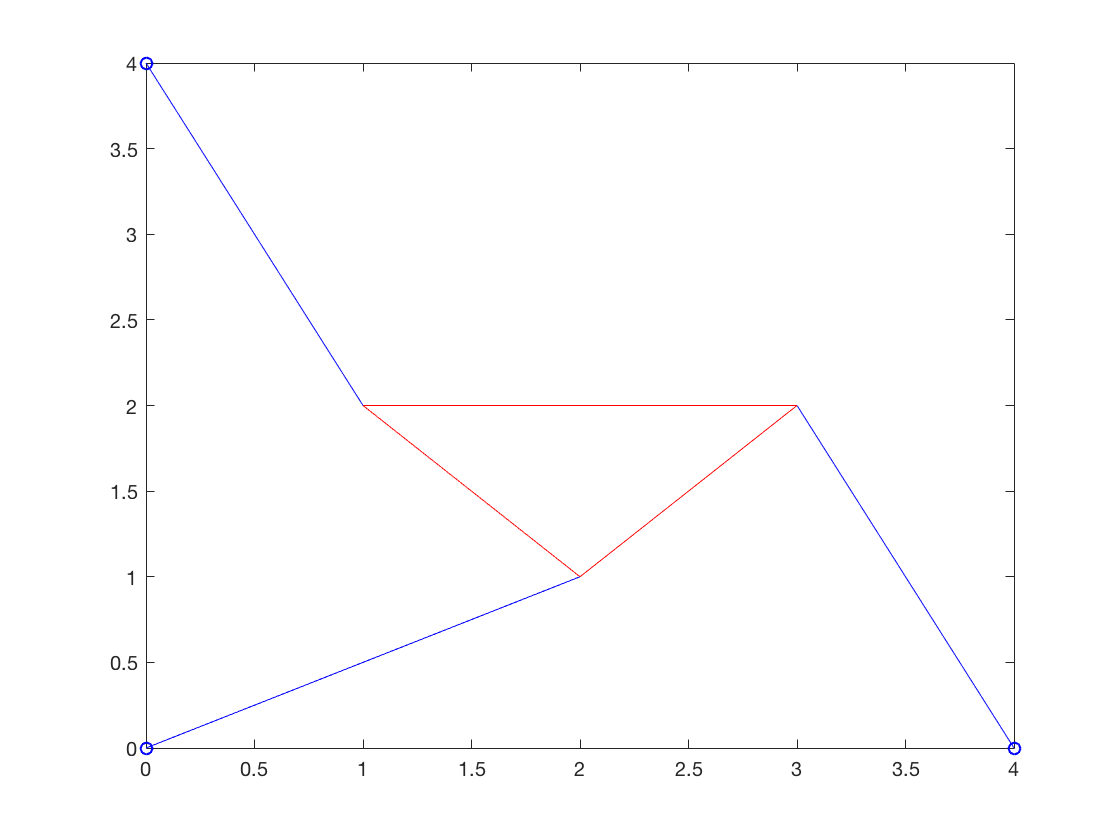
Second Graph

plot([1 2 3 1],[2 1 2 2],'r')
hold on
plot([0 4 0],[0 0 4],'bo')
plot([4 3], [0 2], 'b')
plot([0 1], [4 2], 'b')
plot([0 2], [0 1], 'b')
hold off

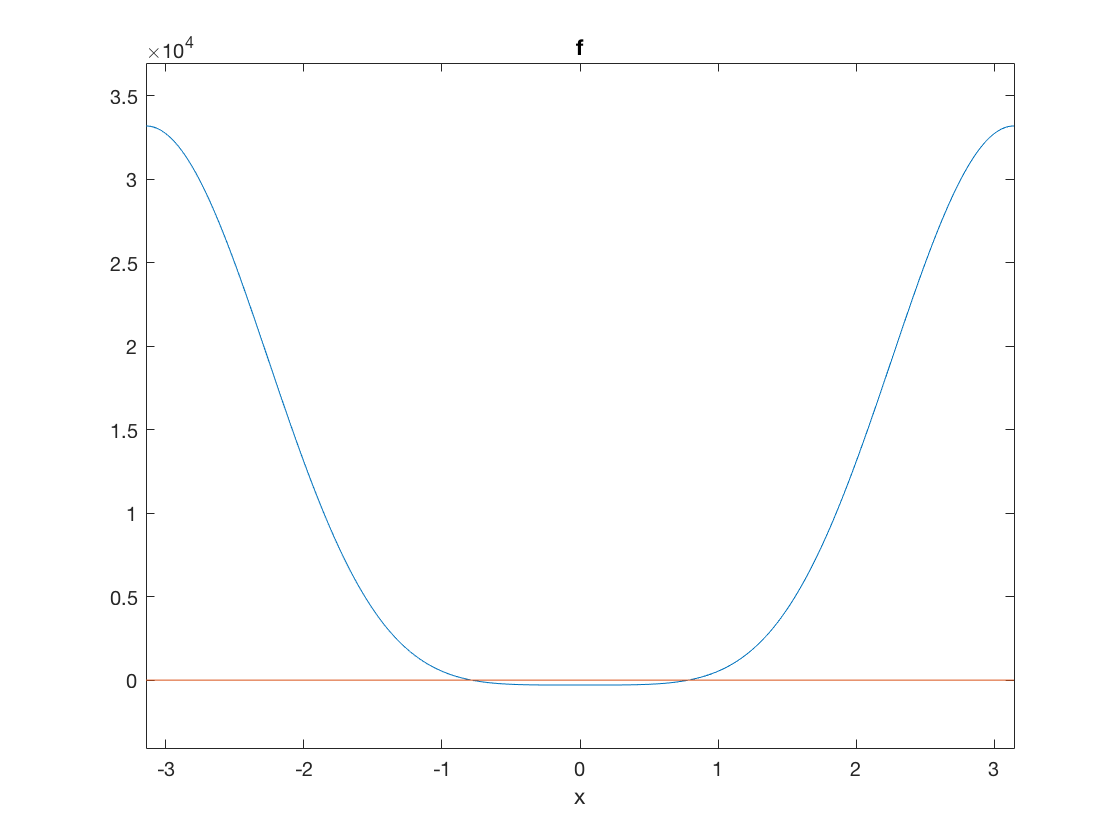
Question Four

Solve the forward kinematics problem for the planar Stewart platform

Fourth Function

Graph

ezplot(@f_4,[-pi,pi])
hold on
plot([-pi,pi],[0,0])
hold off

Warning: Function failed to evaluate on array inputs; vectorizing the function
may speed up its evaluation and avoid the need to loop over array elements.

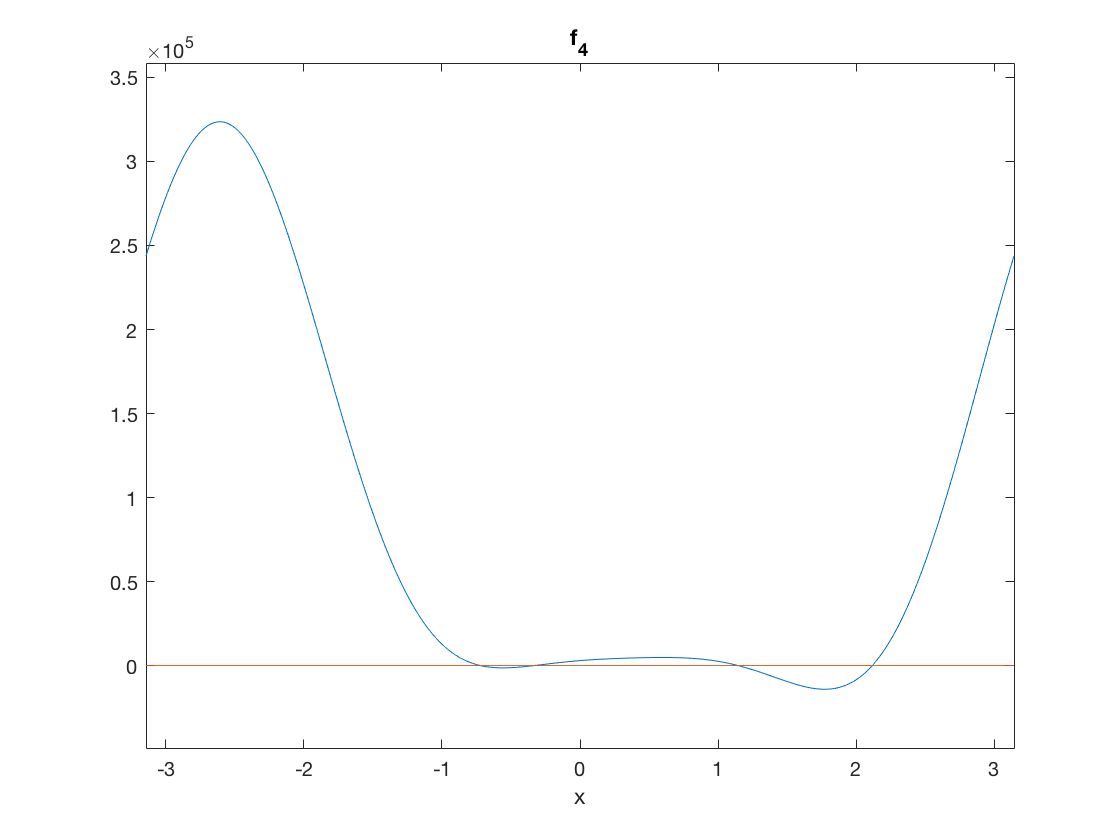
Roots

t1=fzero(@f_4,-0.75)
t2=fzero(@f_4,-0.4)
t3=fzero(@f_4,1.2)
t4=fzero(@f_4,2.1)

Question Five

Change strut length to p2 to some value close to 7 and re-solve the problem. For these parameters, there are six poses

Fifth Function

Graph

ezplot(@f_5,[-pi,pi])
hold on
plot([-pi,pi],[0,0])
hold off

Warning: Function failed to evaluate on array inputs; vectorizing the function
may speed up its evaluation and avoid the need to loop over array elements.

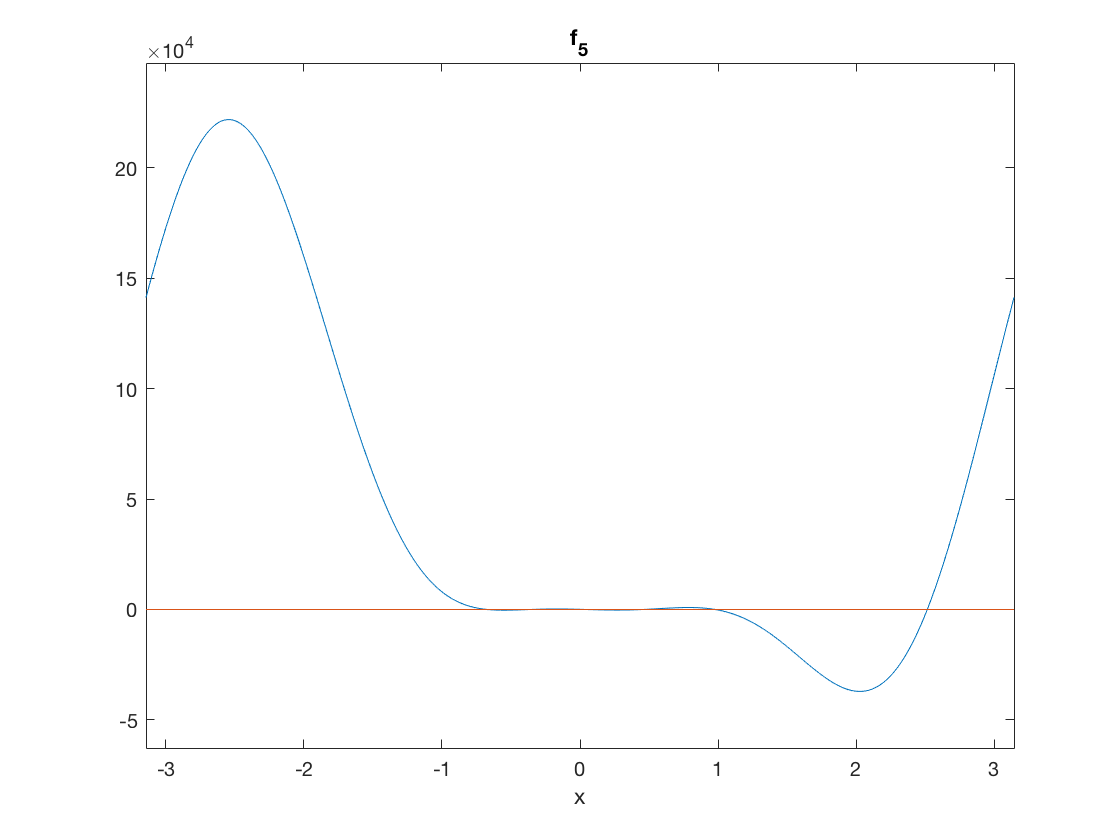
Roots

t1=fzero(@f_5,-0.8)
t2=fzero(@f_5,-0.4)
t3=fzero(@f_5,0.1)
t4=fzero(@f_5,0.5)
t5=fzero(@f_5,1)
t6=fzero(@f_5,2.5)

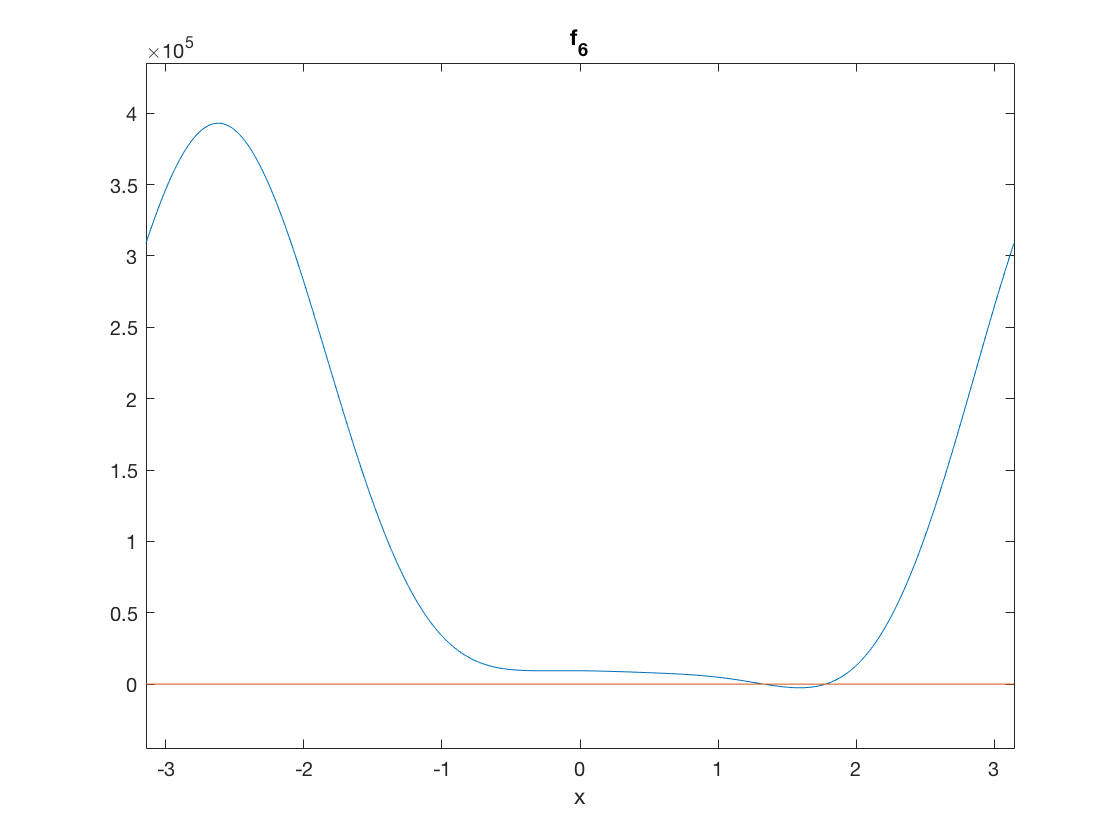
Question Six

Find a strut length p2, with the rest of the parameters as in Step 4, for which there are only two poses

Sixth Function

ezplot(@f_6,[-pi,pi])
hold on
plot([-pi,pi],[0,0])
hold off

Warning: Function failed to evaluate on array inputs; vectorizing the function
may speed up its evaluation and avoid the need to loop over array elements.