Anaxagoras and Philolaus both lived from the early fifth to the late fifth century BCE; Zeno, Melissus, and Empedocles were their contemporaries. Anaxagoras was born in Clazomenae, in Asia Minor; Philolaus was from Tarentum, in southern Italy.

Both had some contact with Athens: Philolaus was the teacher or close associate of some friends of Socrates (469-399 BCE, Athens). Anaxagoras had some association with Archelaus, with whom Socrates was reputed to have studied for a while. Anaxagoras himself visited Athens, and was forced to leave in 432 at the beginning of the religious/political anti-speculation backlash that eventually claimed Socrates' life. However, books by Anaxagoras were apparently readily available in Athens at least as late as 399; see Plato's Apology 26d.

Like other philosophers of their generation such as Melissus and Empedocles, both Anaxagoras and Philolaus seem to have been responding to issues raised by Parmenides and Zeno - issues having to do with whether we can have a coherent account of what exists, or of anything, if we claim that multiple determinate (discrete, identifiable) things exist. Like Empedocles, Anaxagoras and Philolaus do think that it is possible to provide an account of the cosmos in familiar terms, that it is possible to explain what the cosmos is, how it got that way, how there could be multiple things of the types we say exist (rocks, trees, rain), how changes or apparent changes occur, and what goes on when things appear to be generated or destroyed.

Evidence of Parmenides' influence is that later philosophers thought it was of first importance to address the issue of whether there could be multiple things, and why or why not; we have no record of anyone before Parmenides who thought that he or she had to show that there could or could not be multiple things. That later philosophers also thought it crucial to provide evidence or arguments for at least some of their claims is additional testimony to the influence of Parmenides and Zeno.

Philolaus tried to show that multiple things have their source, in some sense, in "the One" or in unity, and that "the One" or unity can itself be analyzed or further understood in some way. Anaxagoras held that even that which appears to be one, or appears to be unified, is really in some way multiple; that there is no smallest bit of anything familiar; and that therefore the problems noted by Parmenides, Zeno, and Melissus can be avoided.

There is more direct evidence that Anaxagoras is responding to Parmenides, Zeno, and/or Melissus (and maybe Heraclitus - note that Anaxagoras is trying to explain the processes or phenomena we call "coming to be" and "passing away", "change", "birth", "death", etc.; all fundamental for H.). This evidence is in the wording of Anaxagoras fragments 5, 6, 8, and 17(13.5, 13.6, 13.8, 13.17 in your text, McKirahan's Philosophy Before Socrates, 2nd ed.); much is close or identical to the Eleatics' wording. Anaxagoras was evidently trying to meet them on their own terms in order to overcome their objections.

---

Anaxagoras of Clazomenae. 

Anaxagoras tried to provide a cosmogony, an account of the development of the cosmos. Unlike Anaximander and Empedocles (and possibly Heraclitus), who conceived of the development process as cyclical; and unlike Anaximenes (and perhaps Heraclitus), who described change within the familiar arrangement of the cosmos as a continual ebb and flow in a variety of directions at once; Anaxagoras described an apparently one-way development of the cosmos as a whole. At least, we have no record of Anaxagoras saying anything about the process reversing, stopping, or repeating. See especially fr. 12 (=13.12 in your text), where he speaks of an "outset" of change (what moves cyclically has no beginning), and of how what brings about the change "will spread further".

At the "outset" of this change (which will eventually result in the development of everyday things, and maybe further development), what exist are evidently "Mind" (Nous) and "seeds" (spermata) (fragments 4, 11-14 [=13.4, 13.11-13.14 in Philosophy Before Socrates 2nd ed.; see also 13.26 and 13.27]). Mind "always is" (fr. 14 [=13.14]).

It's not clear whether Anaxagoras thought that Mind always was as well, but the phrase he uses ('aei esti') can be understood that way. Also, he says that Mind is infinite or unlimited (apeiron) and self-ruling (autokrates). This might be plausibly be taken to mean that it is not limited by anything else (such as having started at a certain time, or having had to be generated by something else), and that it is in no sense dependent on anything else. Anaxagoras may also have thought that the seeds always existed; there's nothing preserved in the fragments to indicate that they came into existence at one point or another.

In Anaxagoras' time, the Greek language was often written without capital letters (except at the beginning of proper names). Thus it is not clear whether 'Nous' (Mind) is supposed to start with a capital. Your text does capitalize, probably to call attention to the important point that Anaxagoras was not saying that an individual human mind is responsible for the generation of the familiar cosmos. Rather, he seems to have meant some sort of cosmic mind, something that pervades the cosmos (frr. 11, 12, 13, 14 [=13.11-13.14; see also 13.28-30]). Individual living things have Mind "in" them (frr. 11, 14), though presumably none of these individual living things contain all of it (none of them can initiate the generation of the cosmos, and they can die, whereas Mind "always is").

Mind brings about the development of familiar things in the following way. It initiates a sort of whirling or revolving which spreads through the mass of seeds, and the seeds collect into various forms, possibly as in a whirlpool or centrifuge (frr. 4, 5, 9, 12, 15-17[=13.4, 13.5, 13.9, 13.12, 13.15-13.17]). To see how that idea might seem plausible, consider what happens if you put food in a blender or food processor and let it run too long: liquid collects at one level, large particles at another level, small ones at another; or denser things go to one level and less dense ones to another; etc.

Mind is distinct from and not mixed with other things, nor does it contain a portion of anything else (frr. 11, 12, 14 [=13.11, 13.12, 13.14]). It can exist where other things are (13.14); Anaxagoras may be saying that it does not take up space in the way that material things do; or he may be saying that since it is so "fine" (i.e. fine-grained; leptos, fr. 12 [=13.12]) it can infiltrate or be "in" other things without mixing them into itself.

The seeds must evidently be imagined as invisibly small particles, no seed quite the same as any other seed (fr. 4 [=13.4]). Everything except Mind is said by Anaxagoras to contain a "portion of everything" (frr. 6, 11, 12 [= 13.6, 13.11, 13.12 in Philosophy Before Socrates 2nd ed.). This suggests that the seeds all contain or are composed of the same stuff, the same "kinds of things", but that each seed contains different proportions of each element or each kind of thing. Anaxagoras appears to be trying to account in this way for certain problematic observations: When we eat vegetables, we do not grow leaves or turn green; and we do develop muscle, bone, flesh, hair, etc. - non-vegetable-like entities. Where did the vegetables and their qualities go? And we don't generally eat bones or hair, yet somehow our bones and hair grow: where did they get the material to do this? If, as Parmenides and others suggested, nothing could be understood to come from nothing, then it seemed likely to many Greek thinkers that things that grew had to have absorbed or accreted something that had previously been external to them. Anaxagoras addresses this at fragments 10 and 17, =13.10, 13.17. Anaxagoras' response to these problems seems to have been that taking in any kind of seeds would allow a thing to grow. We can get taller and heavier (gain bones, muscle, etc.) even from a vegetarian diet because each of the fruits and vegetables we eat is composed of seeds, and the seeds each contain a portion of everything - including flesh, bone, etc. Perhaps an apple, say, does not contain a very large proportion of bone, but that might be why we would have to eat large and varied servings of fruits and vegetables in order to stay healthy. (If this sounds odd, consider that we are told today that we should eat broccoli so as to build strong bones. Bones are largely calcium, and broccoli contains a fair amount of calcium despite the fact that broccoli doesn't look or taste like calcium, much less like bone.)

When the seeds were all together before the revolution started, the mass of seeds had no discernible color, nor was it hot or cold or bright or dark - for the "mixing" of the seeds prevented this (fr. 4 [=13.4]). Possibly what Anaxagoras meant was that because there are little bits of hot (or hot stuff), cold [stuff], bright [stuff], etc. in each seed, none of these qualities predominated in the mass as a whole or in any part of it; and each quality or kind of thing was imperceptible because there was very little of each in any location, and because near each bit was a different of "opposite" bit. That is, no single color would be discernible because any location in the mass would contain seeds of different compositions, and there would not be enough red portions in the seeds in any given location for us to be able to see that the area had red color - and green, blue, black, white, transparent, reflective, and other portions in seeds would be present nearby. Wherever there were bright portions there would also be dark portions; the mixture was such that seeds with large bright portions or large dark portions did not predominate anywhere.

But once Mind got the revolution underway, hot, cold, stars, sun, moon, aer, aither, rare, dense, etc. "separated off" (13.4, 13.5, 13.12, 13.16, 13.17) from the mass. That is, apparently seeds where a certain quality or kind of stuff predominated got together in various spots, perhaps by something akin to centrifuging (13.12). Each familiar thing "is" that of which it contains the most (13.12). What this seems to mean is that what we call "wood" is predominantly wood; what we consider to be a piece of wood is a group of seeds in each one of which  wood portions predominate. To see how this seems to be supposed to work, let us consider what the seeds are supposed to be like. Recall that Anaxagoras holds that there is no smallest thing (13.6) - he is apparently trying to avoid the problems that Zeno showed arose from the supposition that each thing with size is comprised of compounded units. Anaxagoras also holds that each seed contains a portion of everything. What I would suggest that this means is that Anaxagoras is proposing that although familiar things are comprised of seeds, there is no smallest portion of anything in any seed.

Let's look at a seed that would be included in what we call a piece of wood. It has portions of all kinds of stuff, but the largest portion in it is wood. (If it's dry wood, it would also have a good-sized share of the dry,etc.)

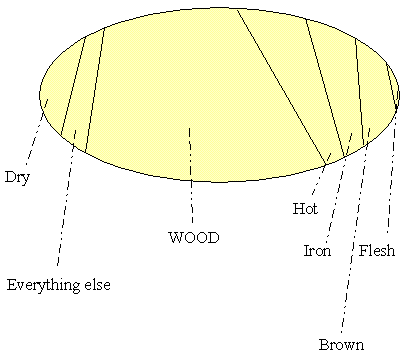
Now let's look at the portion of the seed that is wood. It's only considered to be a "wood portion" because wood predominates.⁽¹⁾  It also contains smaller portions of all other kinds of stuff. (Similarly, each of these smaller portions of other stuff contains a little bit of everything, including wood; the smaller "iron portion" that would be in the predominantly wood seed is only considered to be "iron" because iron predominates in that portion.)

And again, in the "wood portion" of the "wood portion" of the "wood seed", wood predominates, but other ingredients are present also, in smaller quantities. This process of division (or apparent division) within the portions would seem to go on forever - hence there is no smallest bit of wood; each thing that seems to be a small bit of wood, or a portion of a portion of a portion....of a seed will be divisible into smaller portions.⁽²⁾

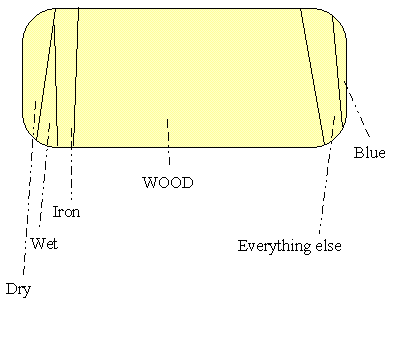
If a bunch of predominantly-wood seeds come together, Anaxagoras proposes, you get a piece of wood. If this agglomeration of seeds gets a bit of Mind caught in it, you get a tree that grows, reproduces, etc. When the tree "dies", the piece of wood decomposes, falls apart, and mixes in with the soil (or, if an animal eats the wood, it mixes with the animal's body, where the bone portions build bone, etc.) Thus, Anaxagoras says, beliefs in "coming into being" and "passing away" are incorrect (17 [=13.17]): things form when seeds "separate off" from the mass (or when later processes in which the early things were involved result in rearrangements); and things change or cease to be what they were when the separated-off pieces decompose and their seeds go into new mixtures.

This ingenious scheme is not without its problems, at least some of which were discovered during or shortly after Anaxagoras' time. One problem is that if there is no pure wood - since all "wood portions" contain sub-portions of other kinds of stuff - then what does it mean to say that something is predominantly wood? That is, in virtue of being predominantly what do we call something "wood"? What exactly makes wood different from other things; what is it to be wood? Something like a paradox of Zeno's, pertaining to what we would call qualities rather than to what we'd call quantities, would seem to arise if we tried to identify or determine what wood was on Anaxagoras' conception.

Another problem was raised by Socrates in Plato's Phaedo. (We don't know whether the historical Socrates actually did this, or whether Plato is using some dramatic license.) Socrates says that he initially thought it was a terrific idea on Anaxagoras' part to give Mind a central role in determining how the universe will be, for this would seem to offer a promising way to account for why things are one way rather than another, for what directions processes and events have taken, and for why at least some aspects of existence seem coherent and regular (recall that Anaxagoras says that Mind understands or grasps all, fr. 12 [=13.12]). But, Socrates complains, Anaxagoras doesn't really make his "Mind" sound like a mind. For "minds" make decisions, based on some awareness of preferences, goals, or values; minds understand things through the things' relevance to an order, and ordering reflects priorities. According to Socrates (and this seems consistent with the surviving fragments of Anaxagoras), Anaxagoras does not address these issues, does not say anything about why Mind does what it does, how and why its decisions (to make things one way rather than another) were made, why it finds one way to be better than another, and so on. These questions would also be important in determining what it would be best for a human to do in any given situation; after all, these matters too are features of what exists. Socrates praises Anaxagoras for acknowledging the issue of purpose or value, but criticizes him for failing to address it adequately (or at all).

---

Philolaus of Croton.  

(This philosopher is also known as Philolaus of Tarentum. Croton and Tarentum were the main Pythagorean communities.)

Philolaus seems to have had among his concerns the implicit challenge raised by the Eleatics regarding the basis on which knowledge would be possible. He seemed to want to account for the relationship between what exists and our knowledge of it; he apparently wanted to try to account for what is believed to exist in such a way as to show that we can have knowledge of that which exists. He tried to do this by fleshing out the Pythagorean ideas of number as a constituent or regulatory feature of what exists, and of the importance of numerical or other mathematical relationships as the key to understanding. Crucially, he seemed to want to claim that we can know that what exists is at least in some respects the way we say it is, on the grounds that (as he sees it) there are fundamental stable features (number, limiting, non-limited⁽³⁾, etc.) that account for the way things are and that can be recognized by us. That is, Philolaus held that numbers (and certain other related stable features of the universe) exist "in" and account for the universe in general. Numbers and these other fundamental stable features account for the way things are, provide principles that can even explain changing phenomena, and can be recognized by us. If we think (in appropriate ways) about things in terms of number, what we think and what is will be the same, and knowledge will be possible, on Philolaus' view.

The question of whether there were stable underlying recognizable features of the universe that accounted for the way things were (or appeared) was of great importance to Plato and to Aristotle, as well as to later thinkers such as the Stoics, the Skeptics, and the neo-Platonists. There was also some concern about whether there could be other conditions under which knowledge or understanding (whatever these might be conceived to be) was possible, and about whether or how we can tell that such conditions were fulfilled.

According to Philolaus' conception, the conditions under which knowledge would be possible were fulfilled. His conception seems to have worked in the following way.

(a)  The ultimate component features of the kosmos are the limiting and the non-limited (fr. 1 [=18.1]; see below for a translation of these fragments).

All things are comprised of the limiting and the non-limited; they need both aspects in order to be determinate things (fr. 3 [=18.3]). (The idea seems to be that if anything was thought to have only a non-limited element it would not be a determinate thing; and that the limiting has to limit something - which would have to be non-limited or else the limiting would not be limiting - in order to be in effect.)

(b) Number takes or has three forms: the odd, the even, and the even-odd (the number one, or the unit: the number one was taken to be the unit out of which all other counting numbers were built). (fr. 5 [=18.5])

Odd numbers are seen as limiting; even numbers are seen as non-limited (see the Burkert reserve reading, or see McKirahan, pages 93-96 and 9.26). The number one, or the unit, is seen as containing both limiting and non-limited (and both odd and even), or as containing the sources of both.

(c) "The One (the number one? unity?) is the beginning or source of everything" (fr. 8; not in McKirahan's Philolaus chapter, but compare 9.26, where Aristotle reports something similar as a position espoused by some Pythagoreans). The One is also the source of all other numbers. (If you are interested in this, start with Heath's A History of Greek Mathematics and Nussbaum's article "Eleatic Conventionalism and Philolaus on the Conditions of Thought" in Harvard Studies in Classical Philology 83 (1979).)

(d) "The nature of number is the cause of recognition" (fr. 11), and is related to harmony (frr. 6 [=18.6], 11). Recognition requires the limiting and the non-limited (fr. 6 [=18.6]).

(e) Thus numbers involve exactly what things involve, in some way or another, so grasping numbers and their relations can (or does) tell us about other things and their relations. Note too that numbers are a feature of human thought and speech (though not only  of human thought and speech, the Pythagoreans would warn); they are not visible or tangible or audible in themselves (you can see or touch what you count to be four objects, and you can see or touch or hear a symbol for the number four, but you don't see or touch or hear four itself), yet they enable us to understand and recognize what is visible or tangible or audible.

A question that arises is whether the limiting and the non-limited, or the odd and the even, or numbers, really have the status Philolaus says they do; and whether or how we can tell. On the other hand, if one is not convinced by Philolaus' account of things (and many in ancient Greece were not), one is left with the interesting questions of why mathematical relations "work" (why proofs are possible; why for any two numbers a and b, a+b=b+a; etc.), and of why at least some observable phenomena in the universe (tides, planetary motions, fulcrums, pendulums) seem to function in ways that are describable mathematically.



(for a complete listing, see K. Freeman, Ancilla to the Pre-Socratic Philosophers)

fragment 1(=18.1 in your text). Nature in the kosmos was fitted together from limiting and non-limited, both the kosmos as a whole and everything in it.

fr. 2. All things that are must necessarily be either limiting [things] or non-limited [things], or both limiting and non-limited [things]. But they could not be merely limiting, nor merely non-limited. Since however it appears that they are neither all from limiting nor all from non-limited, it is clear that the kosmos and the things in it were fitted together from both limiting and non-limited. Things in actions (deeds, works, facts) also show this. For those of them that are from limiting limit, and those that are both from limiting and from non-limited limit and also do not limit, and those that are from non-limited appear non-limited.

fr. 3 (=18.3). For there will not be anything that knows (OR: anything that is known) in the first place if all things are non-limited.

fr. 4. And indeed all things that are known/recognized have number, for it is not possible for anything to be conceived of or known/recognized without this.

fr. 5 (=18.5). Number, indeed, has two kinds (OR: forms) specific to it, odd and even, and a third that comes from (OR: is made out of) mixture of the two, even-odd. Each of the two kinds has many forms, which [forms] each thing in itself indicates.

fr. 6 (=18.6). Concerning nature and harmony this holds: The being of the things (OR: matters, affairs) is eternal and nature itself admits of divine and not human knowledge (OR: recognition), except that it was not possible for any of the things that are and [that] are known/recognized by us to have come to be without there being initially the being of the things from wich the kosmos is composed, both the limiting [things] and the non-limited [things]. And since these principles made the beginning being neither alike (OR: like, same) nor of the same kind, it would have been impossible for them to be ordered (i.e. put into an order), if harmony did not come follow, in whatever way this came to be. The things that were alike/like/same and of the same kind, on the one hand, did not have any need of harmony, but the things that were unlike and not of the same kind and not of equal order, on the other hand - it was necessary for those things to be enclosed together by harmony, if they are to be held together in a kosmos.

(The rest of fr. 6 gives numerical principles for musical harmony, as at McKirahan pp. 92-93.)

fr. 8. The one is the beginning of all things.

fr. 11. (The first few lines of this fragment concern the "decad" or group of the first ten numbers; see Philosophy Before Socrates 2nd ed. pages 92-93 for the basic idea.) Then Philolaus goes on:

For the nature of number is able to give (OR: suited to, related to) recognition/judgment and able to lead and to teach to everyone in what is puzzling and unknown/unrecognized. For none of the things (matters, affairs) would be clear to anyone either in/of itself or in how they are [related] to one another, if there were not number and its being (OR: what is proper to it). Now this (i.e., number) fitting (accommodating? attuning?) all things throughout (OR: in accordance with) soul by means of sense-perception, makes all things known (OR: knowable) and agreeable with one another according to the nature of the gnomon⁽⁴⁾, making them corporeal (? bodies?) and dividing each of the things, both the limiting and the non-limited, separately with respect to their accounts (OR: proportions, measures).

And you may see the nature and power/capability of number prevailing not only in superhuman (daimon-related) and divine matters/affairs/things, but also in all human deeds and words/accounts everywhere, throughout arts and crafts/skills and music.

The nature of number and harmony does not admit of the false at all; for it is not proper (related) to them. The false and ill-will are of a nature to belong to the non-limited and unconceiving (unconceived) and non-rational (unreasoning, unreasoned).

The false does not in any way breathe on (favor? inspire?) number; for the false is opposed and hostile to the nature of number, and truth is proper (related) to and of the same nature as the family of number.

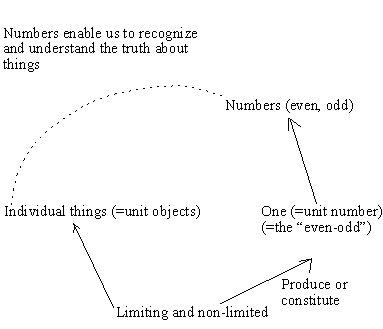
Philolaus' account of what is might be represented something like this: 

---

Notes on Anaxagoras and Philolaus by Rose Cherubin is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License.

Questions, comments?

Contact me at rcherubi(at)gmu(dot)edu.