In this project we looked at solving the reverse Stewart Kinematic problem and graphing the corresponding platforms that various roots form. To do this we set up a function that relied on the value of theta. From here we used the bisection method to find the roots of the function. Once we have the roots for theta we are able to graph platforms.
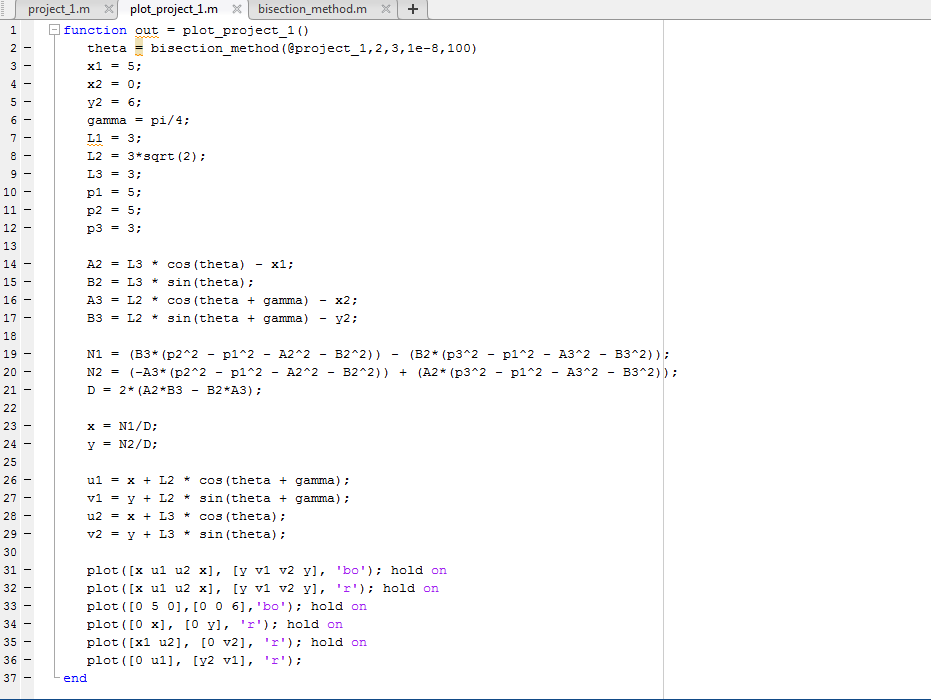
Here are a couple snipets of our code. The first is the general fucntion, the second is the bisection method, and the final one is a function we used to graph the Stewart platforms.


This is the Stewart platform for question 3 figure A and B


This is the graph of theta for problem four and the Stewart platform associated with the four roots, -.7208, -.3310, 1.1437, and 2.1159 respectively.
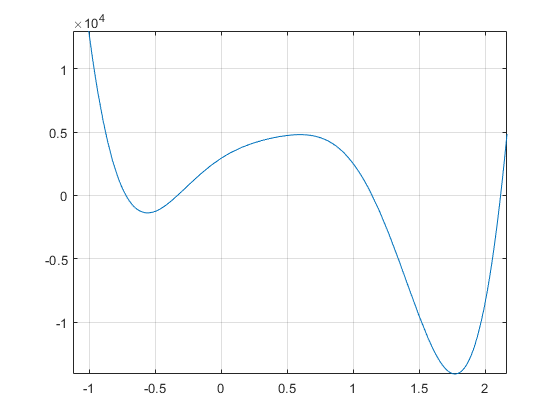




This is the graph of theta for problem five and the Stewart platform associated with the six roots, -.6704, -.3600, .4592, .0399, .4592, .9776, and 2.5140 respectively. We used a p2 length of 7.001 for this problem.







This is the graph of theta for problem six and the Stewart platform associated with the two roots, 1.4416 and 1.775 respectively. We used a p2 length of 4 for this problem. A


