GPS, Conditioning, and Nonlinear Least Square
Group Member: Alex Kayser and Kim Nguyen
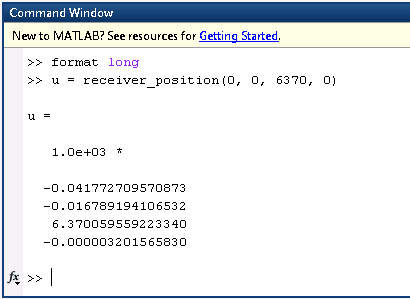
Solve the system (4.37) by using Multivariate Newtons Method. Find the receiver position (x, y, z) near earth and time correction d for known, simultaneous satellite positions (15600, 7540, 20140), (18760, 2750, 18610), (17610, 14630, 13480), (19170, 610, 18390) in km, measured time intervals 0.07074, 0.07220, 0.07690, 0.07242 in seconds, repectively. Set the initial vector to be (x0, y0, z0, d0) = (0, 0, 6370,0). As a check, the answers are approximately (x, y, z) = (-41.77271, -16.78919, 6370.0596), and d = -3.201566*10^-3 seconds.

Write a MATLAB program to carry out the solution via the quadratic formula.
Step 1: Calculate r by using the equation (4.37) on textbook.
Step 2: Assign b = [r15, r25, r35]
Step 3: Assign A = [r11 r12 r13 r14; r21 r22 r23 r24; r31 r32 r33 r34];
Step 4: Then, set r = [A b]. Then using the rref command applied to the augmented matrix [A | b ] returns r.
Step 5: Finally, calculate constant m, d x, y, and z.
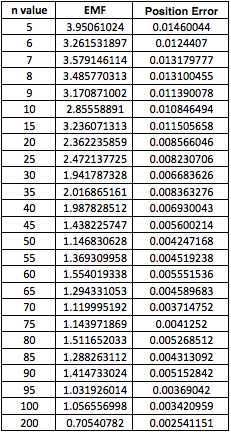
Set up a test of conditioning of the GPS problem. Define satellite positions (Ai, Bi, Ci) from spherical coordinates (ρ φi, θi) where ρ = 26570 km is fixed, 0 ≤ φi ≤ π/2 and 0 ≤ θi ≤ 2π. Compute the difference in position ||(Δx, Δy, Δz)||∞ and the error magnification factor. Try different variations of the Δti's. What is the maximum position error found, in meter? Estimate the condition number of the problem, on the basic of the error magnification factors we have computed.
Repeat step 4 with a more tightly grouped set of satellites. Choose all φi within 5% of one another and all θi within 5 percent of one another. Solve with and without the same input error as Step 4. Find the maximum position error and error magnification factor. Compare the conditioning of the GPS problem when the satellies are tightly loosely bunched.
In this question, we used the same code in part 4 but different input.
Design a Gauss-Newton iteration to solve the least squares system of eight equations in four variables (x, y, z, d). Note that add any number BUT 4 satellites, or investigate adding as many as you want.