Session 1: Probability basics

Full day/on-site

Content Covered

The intent of the first session is to begin thinking about probability by identifying common misconceptions, conducting probability experiments, and developing some fundamental vocabulary. Time will also be spent discussing the process of lesson study. Content discussed will include the following:

Experimental probability
Theoretical probability
Sample space
Events
Law of Large Numbers
Complementary events

Pedagogically, participants will begin looking at alternate forms of assessment and discuss how these can be integrated into a course with an end-of-course SOL test.

Materials Needed

Copies of the handout: “Thinking About Probability”
Dice
Copies of the handout: “Thinking About SKUNK”
Copies of the pretest
Textbooks
Paper clips
Poker chips (two different colors)
Copies of the Spinner handout (text page 421)
Graphing calculators
Projector with internet access

Suggested Problems and Activities

I: Course Overview

It is expected that most participants will have taken Course 1 (Modeling with Algebra and Functions), but some course introduction may be necessary.

II: Thinking about probability—An inventory of prior knowledge

This activity consists of 13 questions, many adapted from questions posed by Fischbein and Schnarch, each of which has an answer that is not necessarily intuitive. It will serve as a good starting point to the course, allowing instructors to get a feel for where the participants are in their thinking about probability. See Appendix A for the answers.

Participants should complete the handouts as quickly as possible, so as to get a feel for their instinctive probability sense. When all participants have finished the handout, the instructors will share the correct answers. The answers are in the appendix of this document.

Instructors may want to read the article “The evolution with age of probabilistic intuitively based misconceptions” (see full citation on the instructional resources page) for more information about the potential misconceptions.

III: The game of SKUNK

NCTM’s illuminations website contains the rules for SKUNK.

Play a few games of SKUNK so that participants can get a feel for the game. Encourage participants to come up with a strategy and stick with it.

Complete the handout: Thinking about SKUNK (available at the above website). The individual strategies should change while completing the handout. Play another game or two of SKUNK and try to determine the optimal strategy.

IV: Pretest (1 ½ hours)

V: Probability experiments (Text section 7.2, P. 419)

Section 7.2 in the textbook outlines 4 different probability experiments. In groups, complete each of the four experiments.

Please note that one of the experiments requires use of the Probability Simulation app. Although this app comes preloaded on the TI-84 calculators, you may need to be prepared with link cables in case some participants do not have this application.

VI: What are the chances? (Text section 7.3, P. 435)

This is a follow-up activity to “Probability Experiments.” It develops the concepts of experimental and theoretical probability and the law of large numbers.

VII: Lesson study video and introduction to lesson study

Homework activities

I. Read the article: “Supporting Reform Through Performance Assessment”

The article outlines the development of performance tasks—what they are and how to score them—by a group of teachers In California.

Participants should write a reflection that addresses the following questions:

“What information about student understanding is gained through performance assessments that cannot be seen in a traditional assessment? With an impending SOL test, do you think performance assessments can realistically be integrated into a core class?”

II. Text Section 7.3: Assignment (page 441). Complete all.

Session 2: Counting Techniques

Online

Content Covered

This session will explore counting techniques, including combinations and permutations, as they relate to determining the total number of outcomes of a probability experiment. Technology will be utilized. Content will include:

Fundamental Counting Principle
Combinations
Permutations
Factorials
Tree Diagrams

Pedagogically, participants will read an article that outlines an assessment strategy that can help improve students’ mathematical communication and better determine if they truly understand the concept being studied.

Materials Needed

Digimemo
Blackboard access/Elluminate Live
Graphing Calculators
Textbooks

Suggested Problems and Activities

I. Discuss responses to the reading “Supporting Reform Through Performance Assessment.”

II. Analyzing Games

This activity, adapted from an activity in Discrete Mathematics Through Applications, poses three different fundraising carnival games. Participants will calculate probabilities and count the number of ways an outcome can occur. Through the activity, participants will develop the fundamental counting process.

At the conclusion of the activity, groups should share their results, in particular the methods they used to count the number of ways the different events could occur. If no one suggests a tree diagram, instructors should share this strategy. Answers to the activity are in the appendix of this document.

III. Photographs and Committees

This article, taken from the February 2000 Mathematics Teacher, walks participants through 3 activities dealing with permutations and combinations. Instructors will want to read the article that accompanies the activity before doing the activity with the class. Instructors may want to assign the reading as homework after completing the activity in class.

IV. Permutations and Combinations, text section 7.9, page 467

This activity serves as a summary of the previous two activities. It formalizes the definition and notation of permutations and combinations and provides examples of each.

Homework activities

I. Text section 7.9: Assignment: Complete all

II. Read the article “A, E, I, O, U and Always Y”

Participants should be prepared to discuss their thoughts on this article in the subsequent session.

Session 3: Combined Events

Online

Content Covered

Participants will refine the probability ideas developed in the first session by looking at more sophisticated methods of determining a sample space. Participants will also be calculating probabilities of combined events and a series of events using formulas developed in the activities. Activities are used that continue to develop counting techniques. Content discussed will include:

Tree diagrams
Venn diagrams
Mutually exclusive events
Complementary events
Addition rule
Independent and dependent events
Multiplication rule
Simulations

Materials Needed

Digimemo
Blackboard access/Elluminate Live
Graphing calculators
Textbooks

Suggested Problems and Activities

I. Discuss responses to the reading “A, E, I, O, U and Always Y”

II. Independent or Dependent?, text section 7.4, page 444.

This lengthy activity explores the additive property of probability, mutually exclusive events, multiplicative rule for probability, dependent and independent events, conditional probability, and Venn Diagrams. At the conclusion of this activity, instructors will want to summarize the distinction between the types of events.

It would also be informative to point out the relationship between mutually exclusive events and independent events. Namely, if events are mutually exclusive, then they are dependent.

III. Name the Event (Enhanced scope and sequence)

This handout provides a list of events, and participants need to describe them as mutually exclusive, independent, dependent, or complementary.

IV. Sounding an Alarm (from Navigating through Probability)

This activity looks at compound events and uses the multiplication and addition principles to calculate probabilities.

Homework activities

I. Text section 7.4: Assignment, page 452: complete all.

II. Read one of the following articles:

“Using Bloom’s Taxonomy as a Framework for Classroom Assessment”

“Portfolios and a Backward Approach to Assessment”

“Using Open-Ended Problems for Assessments”

“Implementing the Assessment Standards: The Myth of Objectivity in Mathematics Assessment”

Participants should reflect on the assessment strategies put forth in their assigned article and be prepared to share their thoughts with small groups in the following class.

Session 4: Conditional Probability

Full day / On-site

Content Covered

In this session, participants will formalize their definition of independent and dependent events by exploring and calculating conditional probabilities. The formula for conditional probability will be discovered and used to enhance the multiplication principle.

Content will include:

Conditional probability
Independent and dependent events
Multiplication Principle
Venn Diagrams

Materials Needed

Copies of the handout “Students with an Earring; Students in Band and Choir”
Copies of the handout “Teaching Probability through Game Shows.”
Copies of the handout “Abby’s Kennels”
Materials to make mystery bags: small paper bags, poker chips, and stickers
Copies of the handout “Independent or Not Independent”

Suggested Problems and Activities

I. Article Discussion

Participants should share their reflections on their assigned article. A jigsaw approach would be appropriate.

II. Students with an Earring; Students in Band and Choir (Enhanced Scope and Sequence)

This activity from the enhanced scope and sequence contains two parts. In the first part, students with an earring, participants are given a Venn diagram consisting of one circle—students with an earring are in the circle, those without an earring are outside. Participants will calculate specific probabilities. The second part consists of a Venn diagram with overlapping circles. Participants will again calculate specific probabilities

III. Teaching probability through game shows

This activity, taken from the April 2005 Mathematics Teacher looks at examples of simple and conditional probability in the price is right. Instructors may want to introduce this activity by showing a clip of Let ‘Em Roll, like this one found on youtube. Instructors should note that this article gets into the concepts of binomial distribution and expected value, which are beyond the scope of Algebra, Functions, and Data Analysis. Therefore, questions 4, 9 and 10 on sheets 3 (a) and (b) may be omitted.

IV. Abby’s Kennels (from Navigating through Probability)

Instructors should reference page 29 of Navigating through Probability for complete description of the activity and for information on how to set up the mystery bags.

V. Independent or Not Independent (from Navigating through Probability)

This activity offers additional practice with conditional probability and identifying independent and dependent events from contingency tables.

VI. The Monty Hall Problem vs. Deal or No Deal

Many participants may be familiar with the famous Monty Hall problem (stick or switch), but I think it is a rule that this problem must be included in any probability course! An extension has been added on to look at the relationship (or non-relationship) between this problem and the current game show, Deal or No Deal. Find answers to the activity in the appendix.

VII. Lesson Study Discussion

Homework activities

I. Text P. 506: Practice Problems. Complete 1 – 5, 8

II. Task creation

Participants should read the article “Provoking Intellectual Need,” thinking about items that differentiate traditional problems from the types of tasks produced in the article. After reading the article they should attempt to create a task in the field of probability that promotes intellectual need.

Session 5: Sampling Methods

Online

Content Covered

This session begins a series of three sessions that focus on designing surveys and experiments. In this session, participants will learn about the different ways a sample can be created and discuss pros and cons of each method.

Content will include:

Sample size
Sampling Techniques
Simple Random Samples
Stratified sampling
Cluster sampling

Materials Needed

DigiMemo
Blackboard Access/Elluminate Live
Graphing Calculator
Textbooks
Text

Suggested Problems and Activities

I. Task Discussion

In small groups, participants should share the tasks they created as a response to the reading “Provoking Intellectual Need.” These should be modified as necessary and shared.

II. Sampling Rectangles (Navigating through data analysis)

III. Sample Size (Navigating through data analysis)

IV. Sampling Methods (Navigating through data analysis)

V. Sampling (TI Activities Exchange)

This simple activity serves as a summary of the previous activities, walking participants through the process of selecting a sample on the calculator.

Homework activities

I. Read the Article: “How do Students Think about Statistical Sampling before Instruction”

Write a short reflection on this article detailing the implications for an Algebra, Functions and Data Analysis course

II. Text P. 583, Section 8.13 Assignment. Complete numbers 1 – 7.

Session 6: Designing Experiments and Surveys

Online

Content Covered

This session builds on the idea of sampling covered in the last lesson and applies it to designing an experiment.

Content will include:

Observational Study
Experiment
Treatment
Control
Placebo
Randomization
Blindness

Materials Needed

DigiMemo
Blackboard Access/Elluminate Live
Graphing Calculator
Textbooks

Suggested Problems and Activities

I. Article Discussion

Discuss responses to reading.

II. We need to Study This. Text section 8.12, page 572

III. Sampling and Bias. Text section 8.13, page 577

IV. Experimental Design, Text page 587, section 8.14

V. What does this study do? (Navigating through data analysis)

Homework activities

I. Text P. 583, Section 8.13 Assignment. Complete numbers 8 – 11.

II. Examining an Article in the News Media (Navigating through Data Analysis)

Session 7: Interpreting Experiments and Surveys

Online

Content Covered

This session continues to build on the concept of sampling in a survey context. In addition, this session provides additional opportunities to think about an experiment or survey’s reliability. Participants will also design an experiment to be carried out an interpreted as homework.

Content will include:

data collection
data analysis/reporting
reducing bias

Materials Needed

DigiMemo
Blackboard Access/Elluminate Live
Graphing Calculator
Textbooks

Suggested Problems and Activities

I. Homework discussion

Groups should share their article with small groups.

II. Sampling: Politics and Opinion (Enhanced Scope and Sequence)

This activity leads participants through the design of a survey to determine how much homework is given in each person’s school. Instructors may choose whether or not to have the groups actually carry out the survey. If they do, they should complete this entire activity. If they do not, they should only complete the exercises 1 – 7.

III. Dietary Change and Cholesterol (Navigating through data analysis)

This activity asks participants to look at a set of data and determine whether modifying a diet helped to lower cholesterol level. They will also connect this topic to probability by conducting a simulation to determine if the results would be likely to do by chance.

Note: Instructors can choose whether to use the more detailed “What can you know—how can you show” or “Data Based Dietary Decisions” to make some initial judgments on the situation. Following the completion of this activity, all should complete “simulating and counting successes.”

IV. Designing a Study (Navigating through data analysis)

Form groups to discuss a topic of interest and design an experiment. Each group will complete the experiment prior to the next class. Groups may choose to meet to conduct the experiment together, or do this individually. Time will be allowed during the next class (designed as an all day face-to-face session) to present the results of the experiment to the class.

Homework activities

I. Text page 591: section 8.14 assignment, 1 – 2

II. Conduct the experiment and interpret results.

Session 8: Summarizing Data

Full day / On-site

Content Covered

In this session, participants will examine different graphs to display data and calculate different measures to summarize data.

Content will include:

Mean
Median
Mode
Range
Interquartile range
Variance
Standard deviation
Outliers

Materials Needed

textbooks
CBRs
meter stick (one per group)
paper plates (one per group)
Graphing calculators
Stopwatch

Suggested Problems and Activities

I. Experiment Presentations

Each group will share the experiment they created and the results with the class.

II. Not-so-small Businesses (Text section 8.1 page 514)

Participants will make observations from a set of data. This activity will set the stage for graphing and analyzing data.

III. What’s in a Name (Text section 8.2 page 516)

This activity introduces a general overview of measures of center and measures of spread.

IV. Get on the stick (TI Activities Exchange)

This activity uses the CBRs and a meter stick to calculate each person’s reaction time. After the data is collected, it is analyzed using a boxplot, illustrating the concepts of median, range, and interquartile range.

V. Transforming Data and Histograms (Text section 8.4 page 529)

In this activity, participants will create boxplots, frequency tables, and histograms and investigate what happens when the data is transformed.

VI. Yankees vs. Mets (TI Activities Exchange)

Participants will make comparisons on two univariate data sets by comparing boxplots and histograms.

VII. How Close is Close? (TI Activities Exchange)

This activity demonstrates different measures of variability, including the variance, standard deviation, and mean absolute deviation. Instructors should note that although mean absolute deviation is not in the AFDA Curriculum that it is in the new standards for Algebra I, so it is recommended that this piece be included.

VIII. Not Your Typical Height (Text section 8.7 page 542).

This activity walks participants through the calculation of standard deviation in a way that is slightly more leading than the previous activity.

IX: Lesson study discussion

Homework activities

I. Text Section 8.4 Assignment. Complete all.

Session 9: The Normal Distribution

Online

Content Covered

This session introduces the normal curve as a family of symmetrical bell-shaped curves that can model many real-life data sets. Participants will look at how the normal curve Is formed, explore special properties of this distribution, and calculate z-scores. This sets the stage for the following session which will challenge participants to calculate the area under a normal distribution.

Content will include:

Normal curve
Mean
Median
Standardized (z) scores

Materials Needed

DigiMemo
Blackboard access/Elluminate live
Graphing calculators
Textbooks

Suggested Problems and Activities

I. z-scores and NFL Quarterback Salaries (Enhanced Scope and Sequence)

This activity serves as an introduction to z-scores which can be used to segue into the subsequent study of normal curves.

II. What’s Normal (Text section 8.8 page 545)

This activity introduces the concept of the normal curve and some of its basic properties.

III. What is a Normal Curve (Enhanced Scope and Sequence)

Participants can either conduct a simulation or use the theoretical probability of the number of heads that occur when tossing a coin ten times to create a frequency curve that is approximately normal.

Homework activities

I. Text section 8.8 assignment, page 555, complete all.

Session 10: Probability and the Normal Distribution

Online

Content Covered

This session will define the area under a normal curve as a way to determine a probability. Participants will also look at the empirical rule and percentiles.

Materials Needed

DigiMemo
Blackboard access/Elluminate live
Graphing calculators
Textbooks

Suggested Problems and Activities

I. Area under the curve (Text section 8.9, page 557)

In this activity students will explore what happens when the mean and the standard deviation of a normal curve is transformed. Area under the curve will be calculated using the graphing calculator, and practical examples are utilized.

II. Areas in Intervals (TI Activities Exchange)

Participants will use their graphing calculator to calculate the area between two values in a normal distribution.

III. Probability Density (Enhanced Scope and Sequence)

This activity provides additional practice with calculating probabilities with normal curves.

IV. Ice Cream Variance (Text section 8.10 page 568)

This activity serves as a culminating activity in the data analysis section. Participants are given 3 data sets of which to make comparisons.

Homework activities

I. Text section 8.9 Assignment, page 566. Complete all.

Session 11: Final Presentations, Summary

Full day / On-site

Content Covered

This session serves as the culminating session of this course. Time should be spent summarizing the entire course, showing where the various segments of course I and course II.

Materials Needed

Copies of post-test

Suggested Problems and Activities

I. Lesson Study Presentations

II. Post-test (1 ½ hours)

III. Applying it in the classroom

Participants should discuss how the elements in courses I and II can best be implemented in the high school AFDA classroom. Time could be spent discussing pacing and design of the AFDA course. Instructors should offer the suggestion of teaching the probability and statistics units at the beginning of the year, reinforcing these ideas throughout the year whenever data is collected.

Appendix A: Answers to Selected Activities

Session 1 Activity:

Thinking About Probability: An Inventory of Prior Knowledge

Answers with explanations:

1: After tossing a coin 10 times, which of the following sequences is most likely to occur?

HTHTHTHTHT or HHTHTTTHTT

Both outcomes are equally likely. A common mistake is to say the 2^nd sequence is more likely to occur because it appears more “random.”

2: In Virginia’s cash 5 lotto, you pick 5 different numbers between 1 and 36. Which of the following has the greatest chance of winning?

4, 5, 12, 20, 36 or 1, 2, 3, 4, 5

Both outcomes are equally likely. As with question 1, the tendency is to choose the first sequence because it appears more “random.”

3: The pick-3 lotto randomly selects three numbers between 0 and 9 (inclusive). On September 11, 2002, the winning number in New York’s Pick-3 lotto was 9-1-1. What is the probability of this happening?

The odds of selecting this combination is 1/1000, just like any other 3 digit combination. An interesting side note: the New York Lottery had to pay out winnings to the more than 5,000 people that selected this combination of numbers.

4: Your friend Bill is flipping a regular coin. You watch the first 20 tosses and are somewhat surprised to see 15 heads. You get bored and leave. When you come back, Bill has tossed the coin a total of 200 times. How many heads do you expect him to have counted?

We would expect him to have 105 heads. To help make sense of this, think about the 200 tosses in terms of the 20 that we saw and the 180 that we didn’t. Of the 20 we saw, we know 15 were heads. Of the 180 we didn’t see, we’d expect (assuming a fair coin) that 90 were heads. The extremely common incorrect response of 100 is most likely due to confusing the relative frequency of an event with the number of times an event will occur.

5: Suppose you toss two coins simultaneously. Which has the greater chance of happening: two heads, two tails, or one head and one tail?

We will most likely see one head and one tail. This can be seen by considering the coins as a nickel and a dime. While there is only one way for two heads or two tails to occur, there are two ways for one of each to occur—either the nickel could be heads while the dime is tails or the dime could be heads while the nickel is tails.

6: Suppose you toss two dice simultaneously. Which has the greater chance of happening: getting two sixes or getting one five and one six?

It is more likely to get one five and one six. The reasoning is similar to that used in question 5.

7: Which is a likelier way to die: to be struck by lightning or to be attacked by sharks?

To figure this out, we actually need data. On average, less than 5 people are killed each year by sharks. About 60 people are killed each year by lightning strikes. The tendency is to answer shark attacks because they are publicized more often than lightning.

8: Is the chance of getting at least 2 tails when tossing a coin 3 times smaller, equal, or greater than the chance of getting at least 200 tails when tossing a coin 300 times?

Because of the law of large numbers, it is much more likely to get at least 2 tails out of 3.

9: About how many people would you need in a room to be fairly certain (say about 90%) that at least two people share a birthday (month and day)?

If there are 40 people in the room, the probability that at least two share a birthday is about 90%.

10: Consider all possible teams of 2 people and 8 people that can be formed from a collection of 10 people. Are there more 2-person teams or 8-person teams, or are there the same number?

There are the same number of 2-person and 8-person teams. A common misconception (even among adults) is that there are more 2-person teams because it is easier to visualize teams of 2 than teams of 8.

11: Suppose you are flipping a coin. How many times would you have to see the same result in a row to be convinced that the coin is biased to one outcome?

This is subjective, of course, but a string of 8 or more in a row is quite unlikely.

12: You have a box containing two white marbles and two black marbles. Without looking, you draw one marble out and see that it is white. Without replacing the marble, you draw a second out. Is it more likely for the second marble to be white or black?

Since there are now one white and two black marbles in the box, it is more likely that the second is black.

13: You have a box containing two white marbles and two black marbles. Without looking, you draw one marble out and set it aside without looking at the color. You then draw a second out and notice it is white. Is it more likely that the first was white or black?

This is essentially the same question is 11. We know that we drew a white marble. Therefore, there are 3 marbles left—2 black and white. It is more likely that a black marble would be chosen from that group.

Session 2 Activity:

Answers:

Analyzing Games

The junior class of Central High School needs to raise $500 to help pay for the senior prom. Three different students have each proposed a different game to be held at the annual school carnival. Read over each proposal, answer the questions, and then give a recommendation to the junior class council.

Pierre’s Proposal

Pierre wants to write each of the letters of the school’s team name, Lions, on a Ping-Pong ball and place them in an opaque container. Participants would pay $1 to draw two balls, one at a time, without replacing the first one when drawing the second. If the letters spell (in the order drawn) a legal word, the participant will win a prize.

1. Some council members criticize Pierre’s proposal because they think it would be too easy to win. Without doing any calculations, what’s your gut reaction towards this criticism?

2. Now let’s analyze the proposal. How many different two-letter “words” are there? How many of them are real words? Use the space below to show how you arrived at your answer.

There are 20 different “words”. Of those, 6 (lo, in, is, on, no, so) are commonly used words, although avid Scrabble players will argue that there are 9 (li, lo, in, is, on, os, no, si, so).

3. If each of the 1,000 students enters exactly once, how many winners would you expect there to be?

If 6/20 is the probability of winning, you would expect there to be 300 winners.

4. How much should each winner receive? Keep in mind the juniors need to raise $500.

If all 1,000 play exactly once, the council will bring in $1,000. They can afford to give $500 back as prizes—each of the 300 winners could receive $1.67 for winning.

Hilary’s Proposal

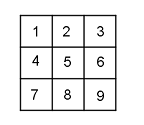
Hilary’s game will involve matching a pair of random numbers. Each participant will pay $1 and receive a square matrix containing integers from 1 to 9. The participant will mark any two of the numbers. A winning pair would be randomly generated. If the participant matches both of the numbers they win a prize.

5. Whereas Pierre’s proposal was criticized for being too easy, some council members think this is too difficult to win and therefore no one will play. What’s your gut reaction to this criticism?

6. Analyze Hilary’s proposal. In how many ways could a student fill in the entry form? Use the space below to show how you arrived at your answer.

There are 36 ways the form could be filled out.

7. If each of the 1,000 students enters exactly once, how many winners would you expect there to be?

We would expect about 28 winners.

8. How much should each winner receive? Keep in mind the juniors need to raise $500.

Each of the 28 winners could receive $18.00 for winning.

Chuck’s Proposal

Chuck’s idea is to give each participant a board with the numbers 1 through 6 displayed. Each participant would buy a chip for $1. The participant would place the chip on any of the numbers on the board, and then roll two dice. He would win $1 for each time the chosen number appeared.

9. Council members think that they may actually lose money on Chuck’s game. What’s your initial reaction?

10. Analyze Chuck’s proposal. In how many ways could the two dice fall? How often would the council pay the participant $1? $2? How often would the council make $1? Use the space below to explain your answers.

Of the 36 ways for dice to fall, 5 of them give $1, 1 gives $2, the remaining 30 give 0.

11. Do you think that the council could raise $500?

If all 1,000 play, we would expect the council to raise over $800.

Making Connections

12. In Pierre’s game, ping-pong balls were drawn one at a time. How many different letters could appear on the first ball drawn? Since this ball was not replaced, how many could appear on the second? What is the connection between these numbers and the total number of “words” that you found earlier?

5 (4) = 20

13. In Hilary’s game, in how many ways could you select the first number? The second? What is the connection between these numbers and the total number of ways the entry form could be filled out? How is this similar and different from Pierre’s game?

9 (8) = 72. Divide by 2 to get 36. This is different from Pierre’s because in Pierre the order matters LI is different from IL. For Hilary, the combination 12 is the same as 21.

14. For Chuck’s game, imagine the two dice are different colors—one red and one green. How many ways could the red die land? The green? What is the connection between these numbers and the total number of ways two dice could fall?

6(6) = 36

15. You’ve probably discovered what mathematicians call the fundamental counting principle. This principle states that if one decision can be done n ways and a second can be done m ways, then the two decisions can be made nm ways. How does this relate to the exercises above?

16. Restate the fundamental counting principle in your own words.

17. Which game would you recommend for the carnival? Explain your reasoning.