Portfolio Review #3

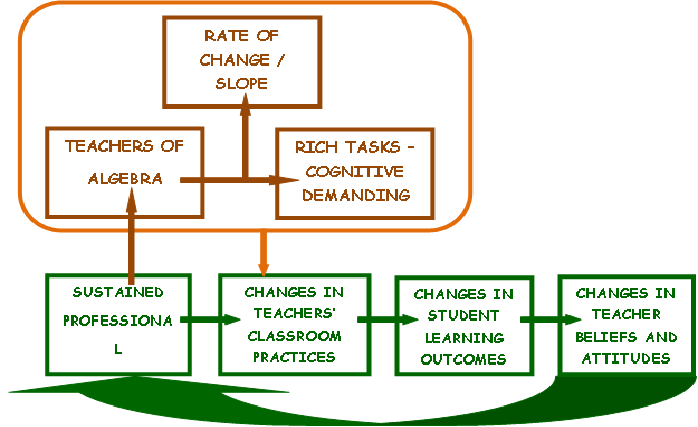
          The concept map for portfolio #2 centered around the influence that leaders had on professional development and the transformation of teachers as they progressed through sessions, gathering evidence of success with new practices, and finally leading to changes in beliefs and attitudes.  My proposed research centers on the professional learning of algebra teachers with regard to rate of change or slope by learning to create and implement rich tasks in their classrooms.  Stump's (1999) research revealed seven representations of slope and the percentage of teachers that acknowledged, practiced, or defined rate of change for each.  Teachers, preservice and inservice teachers, took a pre- and post-test on the content and attended professional learning on the concept.  Her focus was on comparing the two groups of teachers and their knowledge.  My objective would be to focus on content knowledge, pedagogical content knowledge, and how their knowledge or change in conceptual understanding effects their creation of rich tasks and views on teaching the concepts in the classroom.  The ideal situation would be to work with an entire team of algebra teachers in one high school so that the collaboration and team building may continue through the school year.  Zambo and Zambo (2008) discuss teacher's individual efficacy and the collective efficacy of a group of teachers.  Sharing the time during the professional learning as well as increasing their own knowledge was shown to be significant for groups of teachers in low performing schools. 
       Virginia is advocating the teaching of mathematics on the foundation of NCTM Process Standards of communicating, connections, problem solving, representations, and reasoning.  This challenge raises the rigor with instruction.  According to Guskey (2000) teachers need guidance and sustained support in order to change their beliefs about teaching and learning.  This is where the learing and implementation of rich tasks increase in importance.  Rich tasks being a step toward project based learning.  Moylan (2008) posits that there are three "S" goals to project based learning, the development of self, of skills, and to serve society.  NCTM Process Standards and Moylan's "S" goals correlate in the push toward student achievement and positive outlook in mathematics.
     Teachers are also continually challenged with meeting the needs of all students.  Rich tasks will assist in meeting these needs by encouraging students with different models of thinking, learning, and doing mathematics.  Freedman, Delp, and Crawford (2005) stress that rich tasks promotes student thinking by having multiple entry points, multiple paths to solve the problem, and even multiple solutions.        

Portfolio Review #2    

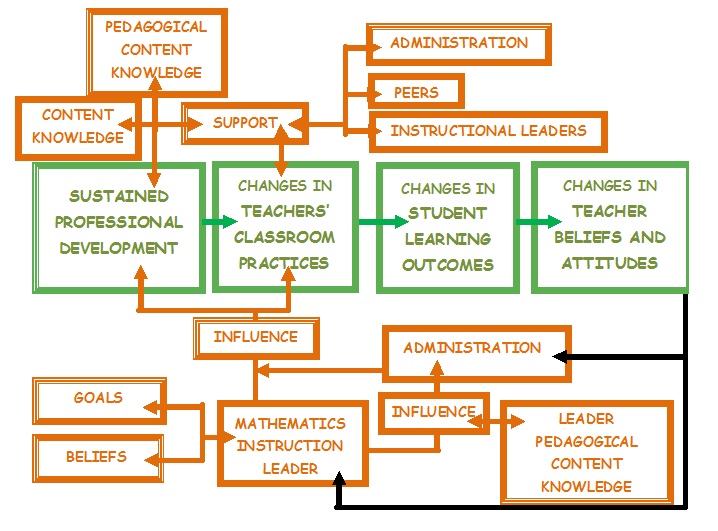
       The above conceptual framework is a modified version of Guskey's (2002) model which is only the green row.
     My interests lie in professional development, standards-based instruction, and the use of graphing technology in the mathematics classroom however my interests have also become more specific.  After delving in to research this past year I have focused on the role that the school district mathematics instructional leader plays in the teacher's journey toward a more standards-based classroom. 
    My hypothesis at this time is that the instructional leader's beliefs and goals for secondary mathematics will align with the NCTM Process Standards but their actions do not uphold their statements.  This is similar to teachers who also feel that they are presenting lessons that are standards-based but when viewed lack substance (Stigler & Hiebert, 1999).  In order for changes in teachers to take place I question whether it actually begins with the instructional leader who guides the school administrators.  With the support of the administration, professional development sessions can then be implemented and Guskey's model will lead to a change in teacher beliefs and attitudes.  The substance of professional development sessions is usually in the hands of the instructional leaders as well.  So how do they view, support, encourage, and oversee the implementation of the items in orange that are above Guskey's model. 
    Changes in teachers begin with mathematics instructional leaders beliefs and goals with respect to:
          * their understanding of the NCTM Process Standards,
          * what standards-based instruction and learning looks like on the secondary level,
          * their ability and opportunity to influence and/or guide administrators,
          * the opportunity to support sustained professional development,
          * their ability to offer content knowledge and pedagogy that supports standards-based learning, and
          * the rapport they have with instructional personnel (trust).

Concept Map and Explanation
Portfolio Review #1
The House That Math Built:
My Original Concept Map

Foundation - Content Knowledge. The foundation, content, in which methods of teaching will be built. One may always add on to the foundation. Learning content continues to occur daily.

Wall Structure - Pedagogy and professional development. Once one has some content knowledge then creativity to apply sound pedagogical practices, along with enhancements obtained through professional development, may be sought and obtained. There are many different methods that teachers may employ but which one is the best for the given situation. It does not happen haphazardly, it takes planning. A "window/door" strategically placed permits teachers to continue to learn through professional development as well as through their own efforts. Inductive approaches, along with direct instruction is shown through research to be the best approach to teaching and learning mathematics. (See Direct Versus Inductive Approaches to Mathematics Instruction).

Roof Structure - Differentiation.  Differentiation methods will pull the wall structure together to form a more sound application so that all students will learn in a safe and secure environment, free to discover the world around them. A student-centered environment aids students as they gain the confidence in the content to go through the door and apply their experiences and knowledge to additional situations. A house may have different roof structures. It is up to the owner to decide what will be best for the family that will live in the dwelling. Likewise, it is up to the teacher to determine the type of differentiation that will be best for the students in his or her classroom. They also need to build the environment so that the students will be receptive. Learning how, what, when, and why teachers need to differentiate instruction will lead to a "structure" that fits well within the environment. 

Heating System - Integrating Technology.  Integration of technology will permit students to learn in a comfortable environment that may meet many of their needs thereby making more of the content obtainable and applicable to their lives. Technology is not the answer to instruction or to differentiation. Teachers need to have the knowledge of how to implement technology in an appropriate manner that will enhance instruction and student learning. This includes the knowledge of how technology fits into the scheme of instruction,and when and how to use technology. During EDRS 810, I came across a study by Kwon (2002) that revealed how the implementation of a Calculator-Based Ranger (CBR), a motion detector used with graphing calculators, encouraged students to become actively involved in learning mathematics (see The Effect of Calculator-Based Ranger Activities on Students' Graphing Ability). Algebra I students were involved in the study along with Calculus students as the control group. The end result was that the Algebra I students understood rate of change and graphing more than the Calculus students. It was not the technology but how the technology was used in the teaching and learning process. Teachers need to be educated on the correct usage of technolgy to aid student learning.

The teacher is the individual that brings the entire "house" together. If open minded and willing to learn teachers can reach all their students.

Back to Top