
|
GROUP PROJECT II |
MATH 447 - Project 2
Authors: Arsah Rahman, Brice Coffman, Maria Pia Younger
Objective: To solve problems 1, 2 (revised version), 4, 5, 6, from Reality Check 4 (Sauer, Pg. 238-241).
- Introduction
- The global positioning system (GPS) consists of 24 satellites carrying atomic clocks, orbiting the earth at an altitude of 20,200 km (twice per day)
- The GPS constellation consists of 24 satellites in 6 orbital planes with 4 satellites in each plane.
- The ascending nodes of the orbital planes are separated by 60 degrees and the planes are inclined 55 degrees.
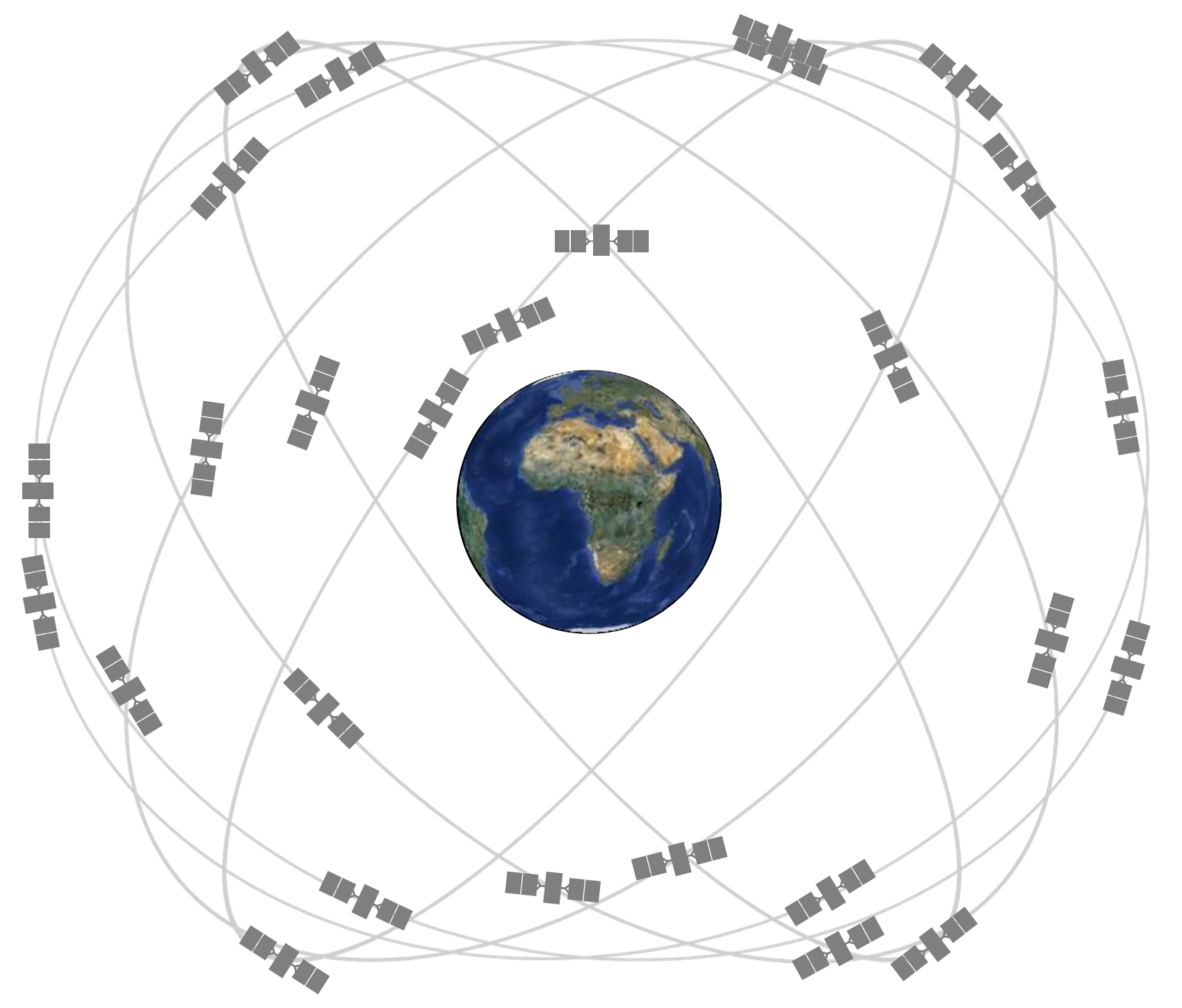
- At any time, from any point on earth, five to eight satellites are in the direct line of sight

- Each satellite's mission is to transmit carefully synchronized signals from predetermined positions in space, to be picked up by GPS receivers on earth.
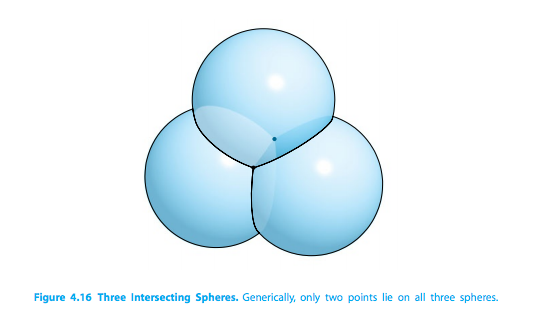
- This receiver can tell where each satellite is by time lag; each satellite makes a sphere with these time lags, and whereever these three spheres meet, that is where the accurate location on earth is.

- Activities
-
Multivariate Newtons Method [Check Code Here!]
Find the receiver position (x, y, z) near earth and time correction d for known, simultaneous satellite positions (in km):
(15600km, 7540km, 20140km, 0.07074s),
By Solving (Eq. 4.37):
(18760km, 2750km, 18610km, 0.07220s),
(17610km, 14630km, 13480km, 0.07690s),
(19170km, 610km, 18390km, 0.07242s)\(r1 = (x, y, z, d) = \sqrt((x-A1)^2+ (y-B1)^2 + (z-C1)^2) - c*(t1-d) = 0;\) \(r2 = (x, y, z, d) = \sqrt((x-A2)^2+ (y-B2)^2 + (z-C2)^2) - c*(t2-d) = 0;\) \(r3 = (x, y, z, d) = \sqrt((x-A3)^2+ (y-B3)^2 + (z-C3)^2) - c*(t3-d) = 0;\) \(r4 = (x, y, z, d) = \sqrt((x-A4)^2+ (y-B4)^2 + (z-C4)^2) - c*(t4-d) = 0;\)
Solution (Eq. 4.38):\(r1 = (x, y, z, d) = (x-A1)^2+ (y-B1)^2 + (z-C1)^2 - [c*(t1-d)]^2 = 0;\) \(r2 = (x, y, z, d) = (x-A2)^2+ (y-B2)^2 + (z-C2)^2 - [c*(t2-d)]^2 = 0;\) \(r3 = (x, y, z, d) = (x-A3)^2+ (y-B3)^2 + (z-C3)^2 - [c*(t3-d)]^2 = 0;\) \(r4 = (x, y, z, d) = (x-A4)^2+ (y-B4)^2 + (z-C4)^2 - [c*(t4-d)]^2 = 0;\)
Set the initial vector to be (x0, y0, z0, d0) = (0km,0km,6370km,0s) and check if the answers are approximately (x, y, z) = (−41.77271,−16.78919,6370.0596), and d = −3.201566 × 10−3 seconds.
Results:ans =
1.0e+03 *
-0.041772709570893
-0.016789194106523
6.370059559223352
-0.000003201565830
-
Get a quadratic equation in one variable "d" [Check Code Here!]
Write a MATLAB program to solve the problem in Step 1 via the quadratic formula
Solution:
We substracted the last three equations of (Eq. 4.38) from the first equation, which yielded three linear equations in the four unknowns u = [x, y, z, d], or in matrix form, Au = b where A is a 3 × 4 matrix (as the book suggested us to do).
\begin{array}{cccc|c}1&0&0&r14&r15\\0&1&0&r24&r25\\0&0&1&r34&r35\end{array}
Giving expressions:
\(x = -r14d + r15;\)
\(y = -r24d + r25;\)
\(z = -r34d + r35;\)
Results:
d = -0.003201565829594;
x = -41.77270957083570835708;
y = -16.789194106525994;
z = 6.370059559223344e+03;
- Set up a test of the conditioning of the GPS problem. Define satellite positions
(Ai,Bi,Ci) from spherical coordinates \((\rho i,\phi i, \theta i)\) as:
\(Ai = \rho*cos(\phi i)*cos(\theta i)\)
\(Bi = \rho*cos(\phi i)*sin(\theta i)\)
\(Ci = \rho* sin(\phi i)\),
Where:
\(\rho= 26570km\);
\(0\leq\phi i\leq\pi/2\);
\(0\leq\theta i\leq\pi\);
and \(i = {1,2,3,4}\) are chosen arbitrarily,
\(x = 0; y = 0; z = 6370; d = 0.0001\);
\[Ri = sqrt(Ai^2+ Bi^2 + (Ci^2 - 6370)^2)\]
ti = d + Ri/c;
Thetas used: \(\pi/3, \pi/8, \pi/4, \pi/2\);
Phies used: \(\pi/3, \pi/8, 3*\pi/4, 2*\pi\);
Since the atomic clocks aboard the satellites are correct up to about 10ns. We decided to vary time randomly with a \(\pm\) 10^-8 difference in each clock.
Solving:
\[\begin{equation*} emf = \frac{||(\Delta x, \Delta y, \Delta z)||_{\infty}}{c||\Delta t_{i}||_{\infty}} \end{equation*}\]
Results (Error Magnification Factor):
ans =
4.553308261063736
Five Percent Distance Difference[Check Code Here!]
Repeat step with a more tightly grouped set of satellites. Choose all \(\phi i\) within 5 percent of one another and all \(\theta i\) within 5 percent of one another. Solve with and without the same input error as in Step 4. Find the maximum position error and error magnification factor. Compare the conditioning of the GPS problem when the satellites are tightly or loosely bunched.
Solving For:
We used different thetas and phies to ensure they did not passed their limit-value. Thetas used: \(\pi/3, \pi/8, \pi/5, \pi/4\);
Phies used: \(\pi/3, \pi/8, 3*\pi/8, 3*\pi/5\);
Results With No Time Error:
Results show that we converge to the real values
u =
1.0e+03 *
-0.000000000018391
0.000000000029287
6.369999999972432
0.000000100000000
emf =
9.769044938636306e-06
maxEMF =
9.769044938636306e-06
ans =
9.769044938636306e-06
Results with Time Error:
Results show that we are really off the real value. The emf and maxEMF shows the same results. u =
1.0e+03 *
0.052981663460079
-0.084653992948943
6.449654432148920
0.000000208993703
emf =
2.823753256292495e+04
maxEMF =
2.823753256292495e+04
ans =
2.823753256292495e+04
-
More Satellites[Check Code Here!]:
Decide whether the GPS error and condition number can be reduced by adding satellites. Return to the unbunched satellite configuration of Step 4, and add four more. (At all times and at every position on earth, 5 to 12 GPS satellites are visible.) Design a Gauss–Newton iteration to solve the least squares system of eight equations in four variables (x, y, z, d). What is a good initial vector? Find the maximum GPS position error, and estimate the condition number. Summarize your results from four unbunched, four bunched, and eight unbunched satellites. What configuration is best, and what is the maximum GPS error, in meters, that you should expect solely on the basis of satellite signals?# of Satellites Output with no time variable Output with time variable of 10^-8 8 5.460745991119200e-09 4.744452309891821 9 4.160073430158780e-09 6.438043311323899 10 9.101243318532000e-10 2.689372038816007 11 1.213499109137600e-09 3.579006477346765 12 1.460059424682655e-09 2.689625730816140