---

IMAGE COMPRESSION:   using the Two-Dimensional Discrete Cosine Transform (2D-DCT)

                           and Quantization Methods

Roadmap to Image Processing:

1. B&W Image
1. Encode Image (Matrix \(X\))
1. Convert int to double
2. Center (offset (128) subtracted)
3. 2D-DCT Applied: \( Y = C X C^{T}\)
4. Quantization Applied ("loss parameter p"): \(Yq=round(Y./Q\))
2. Recover Image (Matrix \(X\))
1. De-Quantization Applied: \(Ydq=Yq.*Q\))
2. Inverse 2D-DCT Applied: \(X = C^{T} Y C\)
3. Center (offset (128) added)
4. Convert double to int (uint8)
2. Color Image
1. Encode Image (Matrix \(X\))
1. Convert int to double
2. Center (offset (128) subtracted)
3. Convert RBG Color Data to YUV System
4. 2D-DCT Applied
5. JPEG Quantization Applied: Convert YUV System to "Baseline JPEG" for Luminance & Color Differences utilizing \(Q_{Y}\) & Color Difference \(Q_{C}\) Matrices
2. Recover Image (Matrix \(X\))
1. De-Quantization Applied to "Baseline JPEG" (backout Quantization)
2. Inverse 2D-DCT Applied
3. Transform YUV System back to RGB Color Data
4. Center (offset (128) added)
5. Convert double to int (uint8)

Real, Orthogonal Matrix C:

$$C_{ij} = \frac{\sqrt 2}{\sqrt n} a_{i} \text{cos} \frac{i(2j+1)\pi}{2n}$$ for \(i,j=0,...,n-1\), where $$a_{i} \equiv \begin{cases} \frac{1}{\sqrt 2}, & \mbox{if } \mbox{ i=0,} \\ 1, & \mbox{if } \mbox{ i=1,...,n-1} \end{cases}$$ or $$C = \sqrt{\frac{2}{n}}\left[\begin{matrix} \frac{1}{\sqrt2} & \frac{1}{\sqrt2} & \cdots & \frac{1}{\sqrt2} \\ \text{cos}\frac{\pi}{2n} & \text{cos}\frac{3\pi}{2n} & \cdots & \text{cos}\frac{(2n-1)\pi}{2n}\\ \text{cos}\frac{2\pi}{2n} & \text{cos}\frac{6\pi}{2n} & \cdots & \text{cos}\frac{2(2n-1)\pi}{2n}\\ \vdots & \vdots & & \vdots \\ \text{cos}\frac{(n-1)\pi}{2n} & \text{cos}\frac{(n-1)3\pi}{2n} & \cdots & \text{cos}\frac{(n-1)(2n-1)\pi}{2n} \end{matrix} \right] $$

2D-DCT ===> \(Y=CXC^{T}\) Image Matrix X ===> \(n\times n\) matrix \(X\) matrix , where \(C\) is defined as: $$C_{ij} = \frac{\sqrt 2}{\sqrt n} a_{i} \text{cos} \frac{i(2j+1)\pi}{2n}$$ for \(i,j=0,...,n-1\), where $$a_{i} \equiv \begin{cases} \frac{1}{\sqrt 2}, & \mbox{if } \mbox{ i=0,} \\ 1, & \mbox{if } \mbox{ i=1,...,n-1} \end{cases}$$ or $$C = \sqrt{\frac{2}{n}}\left[\begin{matrix} \frac{1}{\sqrt2} & \frac{1}{\sqrt2} & \cdots & \frac{1}{\sqrt2} \\ \text{cos}\frac{\pi}{2n} & \text{cos}\frac{3\pi}{2n} & \cdots & \text{cos}\frac{(2n-1)\pi}{2n}\\ \text{cos}\frac{2\pi}{2n} & \text{cos}\frac{6\pi}{2n} & \cdots & \text{cos}\frac{2(2n-1)\pi}{2n}\\ \vdots & \vdots & & \vdots \\ \text{cos}\frac{(n-1)\pi}{2n} & \text{cos}\frac{(n-1)3\pi}{2n} & \cdots & \text{cos}\frac{(n-1)(2n-1)\pi}{2n} \end{matrix} \right] $$

1. Computer Problem 11.2.3(a-e): Extract an 8x8 pixel; apply 2D-DCT; Quantize using linear quantization \(p=1,2,4\); Print out each \(Y_{Q}\); Reconstitute image.

Result (a): 8\(\times\)8 pixel block (Matlab code)

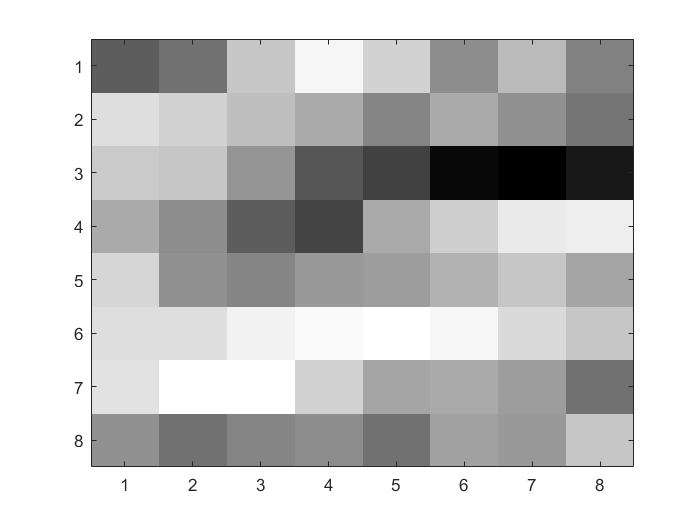	Original B&W	8x8 Pixel

Result (b,c,d):Apply 2D-DCT; Quantize using linear quantization \(p=1,2,4\); Print out each \(Y_{Q}\);

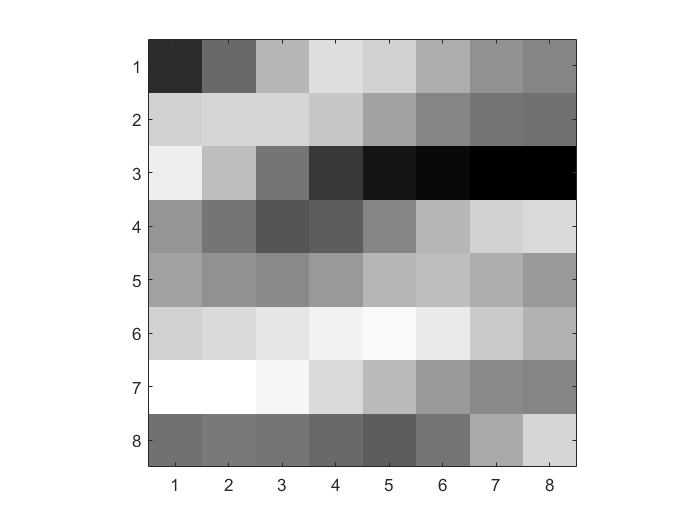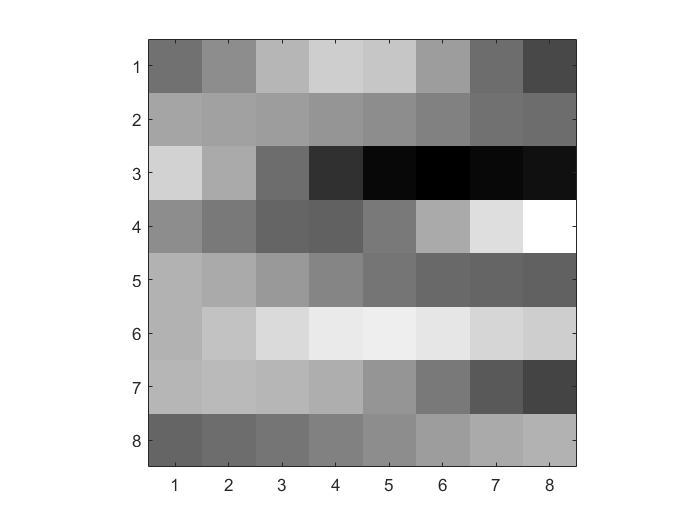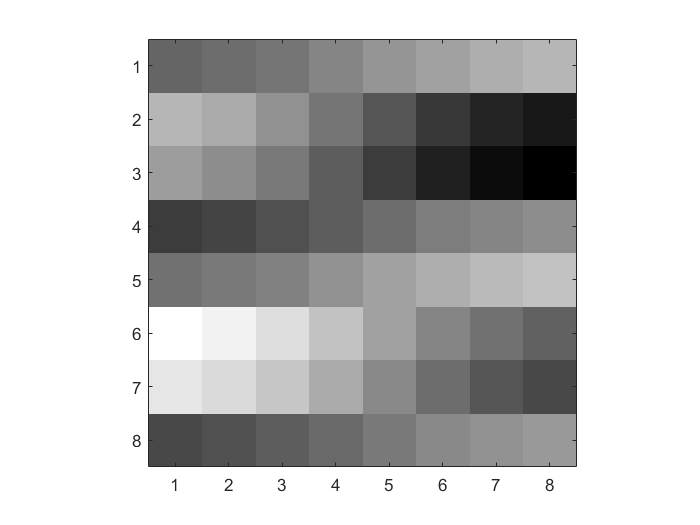	p = 1 \(Y_Q\) Linear Quantization (p=1)	p = 2 \(Y_Q\) Linear Quantization (p=2)	p = 4 \(Y_Q\) Linear Quantization (p=4)

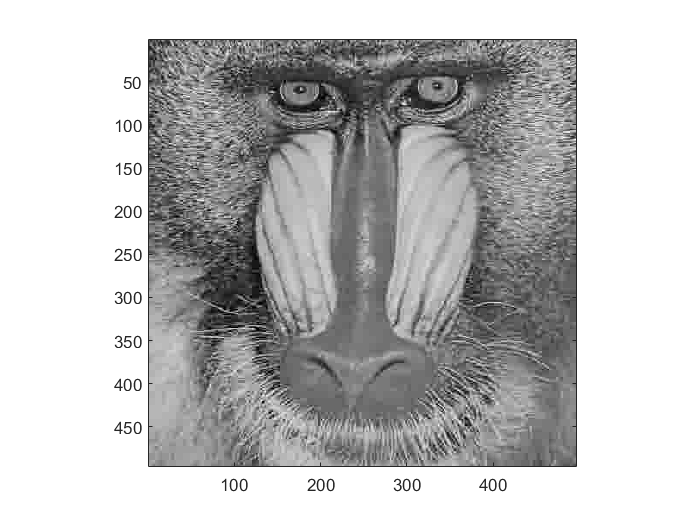
Result (e):Reconstitute image;(Matlab code)

	Original B&W	p = 1	p = 2	p = 4

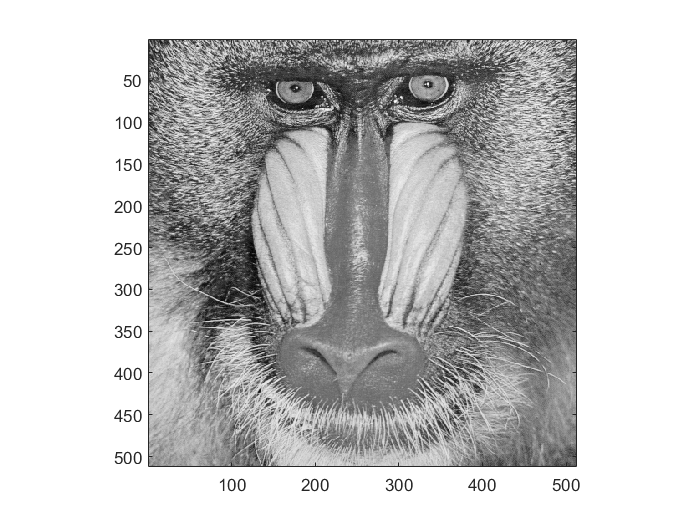
2. Computer Problem 11.2.4: Special Matrix for Quantization \(Q_{Y}\) with \(p=1\)

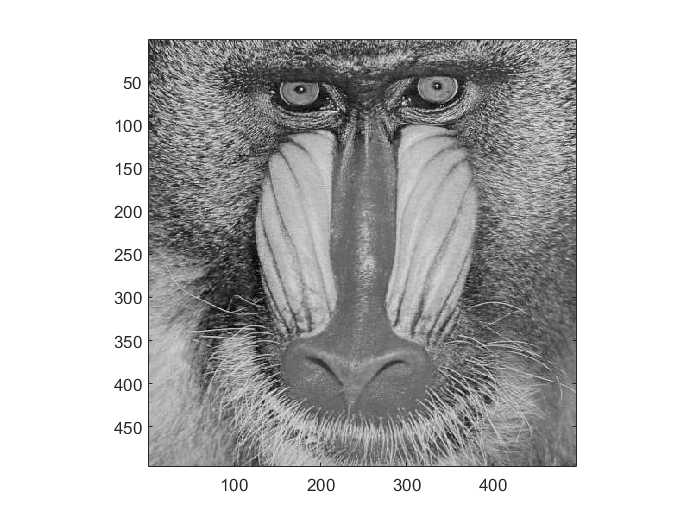
Result: Impressive Reconstruction (Matlab code)

	Original B&W	Special Quantization Matrix \(Q_{Y}\) JPEG Quantization \(Y_Q\) (p=1)

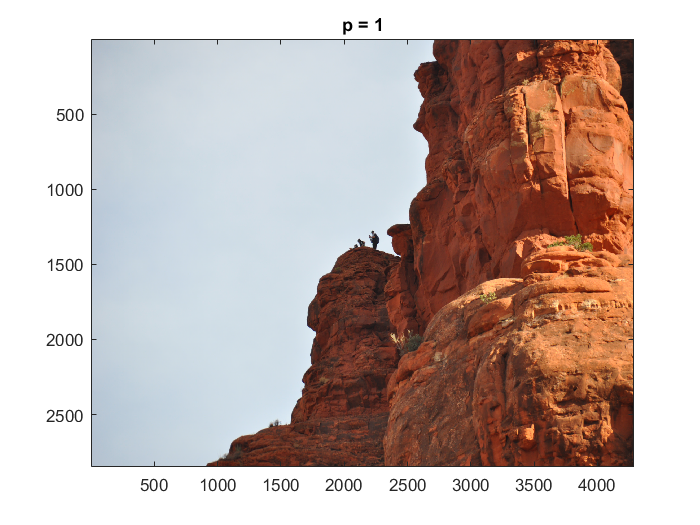
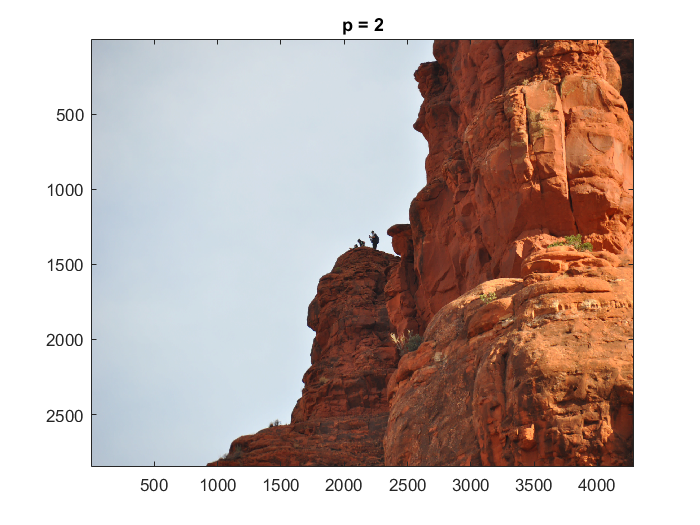
3. Computer Problem 11.2.5: Color Image

Results: (Matlab code)

	Sedona, AZ	p=1 RGB \(Y_Q\) (p=1)	p=2	p=4

	p=16

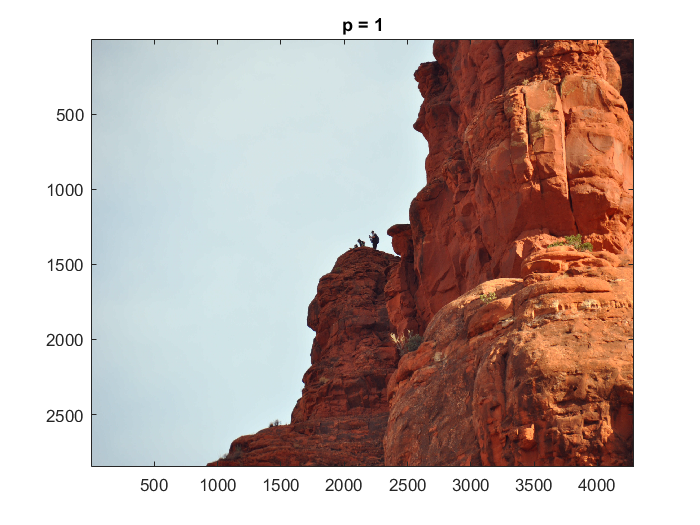
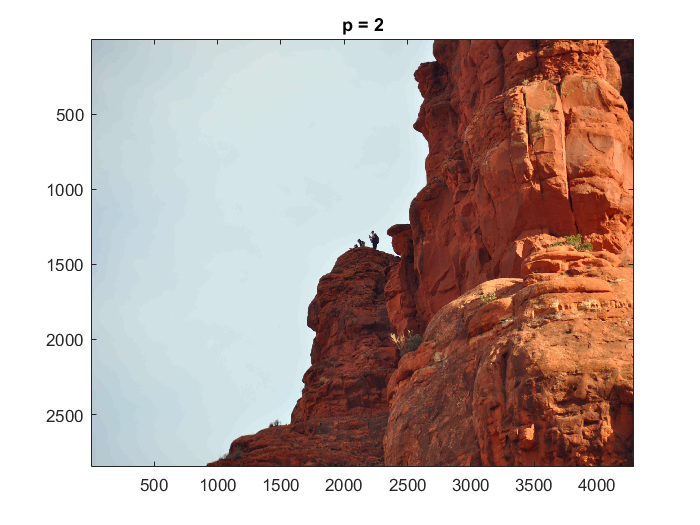
4. Computer Problem 11.2.6: Color Image - Transform RGB-to-YUV (Luminance \(Q_{Y}\) & Color Difference \(Q_{C}\))

Results: (Matlab code)

	Sedona, AZ	p=1	p=2	p=4
	Original	Luminance \(Q_{Y}\) & Color Difference \(Q_{C}\)	Luminance \(Q_{Y}\) & Color Difference \(Q_{C}\)	Luminance \(Q_{Y}\) & Color Difference \(Q_{C}\)

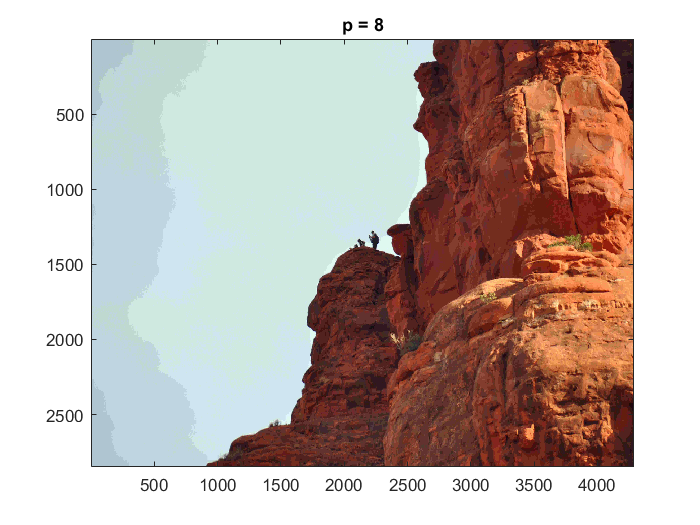	p=8