MATH 447 (Numerical Analysis II)
Project 2: GPS, Conditioning, and Nonlinear Least Squares
===> Wyatt Rush, Brandon Scott, Mike Sullivan <===
"Numerical Analysis" (3rd Edition; 2018), P248-251: Reality Check 4
Four (4) Equations; Four (4) Unknowns
- \[ r_{1}(x,y,z,d) = \sqrt{(x-A_{1})^2 + (y-B_{1})^2 + (z-C_{1})^2} { - c(t_{1}-d) = 0} \]
- \[ r_{2}(x,y,z,d) = \sqrt{(x-A_{2})^2 + (y-B_{2})^2 + (z-C_{2})^2} { - c(t_{2}-d) = 0} \]
- \[ r_{3}(x,y,z,d) = \sqrt{(x-A_{3})^2 + (y-B_{3})^2 + (z-C_{3})^2} { - c(t_{3}-d) = 0} \]
- \[ r_{4}(x,y,z,d) = \sqrt{(x-A_{4})^2 + (y-B_{4})^2 + (z-C_{4})^2} { - c(t_{4}-d) = 0} \]
Part 1: Multivariate Newton's Method (Nonlinear Systems of Equations)
===> Newton-Taylor-Jacobi Nexus <===
Taylor Expansion for Vector-Valued Functions around x0
Jacobian Matrix
Matlab Backslash "\": ("Matrix Left Division")
===> Matrix Inverses: Computational-Intensive
- \[ x_{0} = Inital Vector \]
- \[ x_{k+1} = x_{k} - (DF(x_{k}))^{-1} * F(x_{k}) \]
===> Modification:
- \[ DF(x_{k}) * s = - F(x_{k}) \]
- \[ x_{k+1} = x_{k} + s \]
Multivariate Newton's Method Code (DriverP1.pdf)
Multivariate Newton's Method Code (MultivariateNewtonP1.pdf)
Multivariate Newton's Method ("Top-of-the-World") |
||||
|---|---|---|---|---|
| Iteration | x | y | z | d |
| 0 | 0 | 0 | 6370 | 0 |
| 1 | -41.773366868922 | -16.751057066684 | 6375.183134528647 | -0.003262714514 |
| 2 | -41.772709784019 | -16.789181734793 | 6370.061221318984 | -0.003201585666 |
| 3 | -41.772709570810 | -16.789194106508 | 6370.059559223537 | -0.003201565830 |
| 4 | -41.772709570810 | -16.789194106509 | 6370.059559223361 | -0.003201565830 |
| 5 | -41.772709570824 | -16.789194106523 | 6370.059559223344 | -0.003201565830 |
| 6 | -41.772709570995 | -16.789194106585 | 6370.059559223278 | -0.003201565830 |
| 7 | -41.772709570824 | -16.789194106523 | 6370.059559223344 | -0.003201565830 |
Multivariate Newton's Method (*** STRESS TEST #1: Center-of-Earth ***) |
||||
|---|---|---|---|---|
| Iteration | x | y | z | d |
| 0 | 0 | 0 | 0 | 0 |
| 1 | -41.746231027747 | -18.325503550146 | 6163.661863983135 | -0.00738257158 |
| 2 | -41.773065120405 | -16.768564803099 | 6372.831032582411 | -0.003234642722 |
| 3 | -41.772709633321 | -16.789190485500 | 6370.060045698348 | -0.003201571636 |
| 4 | -41.772709570787 | -16.789194106518 | 6370.059559223369 | -0.003201565830 |
| 5 | -41.772709570835 | -16.789194106526 | 6370.059559223349 | -0.003201565830 |
| 6 | -41.772709570806 | -16.789194106521 | 6370.059559223347 | -0.003201565830 |
| 7 | -41.772709570820 | -16.789194106523 | 6370.059559223348 | -0.003201565830 |
Multivariate Newton's Method (*** STRESS TEST #2: 2 * Earth's Radius ***) |
||||
|---|---|---|---|---|
| Iteration | x | y | z | d |
| 0 | 0 | 0 | 12740 | 0 |
| 1 | -41.742184136241 | -18.560307920714 | 6132.116734114572 | -0.00361773342 |
| 2 | -41.773184055048 | -16.761664097852 | 6373.758117716814 | -0.003245707268 |
| 3 | -41.772709681913 | -16.789187658476 | 6370.060425493047 | -0.003201576168 |
| 4 | -41.772709570761 | -16.789194106502 | 6370.059559223419 | -0.003201565830 |
| 5 | -41.772709571090 | -16.789194106612 | 6370.059559223251 | -0.003201565830 |
| 6 | -41.772709570764 | -16.789194106502 | 6370.059559223368 | -0.003201565830 |
| 7 | -41.772709570949 | -16.789194106555 | 6370.059559223320 | -0.003201565830 |
Multivariate Newton's Method (*** STRESS TEST #3: Earth-Moon Distance = 238,855 miles = 384,399.861 km ***) |
||||
|---|---|---|---|---|
| Iteration | x | y | z | d |
| 0 | 0 | 0 | 384399.861 | 0 |
| 1 | -73.5651091496 | 1827.8350950296 | 254188.7548370616 | -2.9608602762 |
| 2 | -57.1783144346 | 877.0581799044 | 126455.2667810744 | -1.4363906912 |
| 3 | -49.00051046443 | 402.57446420118 | 62710.07159585218 | -0.67560655592 |
| 4 | -44.94258837915 | 167.13009244919 | 31078.95984792500 | -0.29809656591 |
| 5 | -42.97397392401 | 52.90926957537 | 15733.79960864720 | -0.11495563381 |
| 6 | -42.098642567295 | 2.121738359980 | 8910.675899345410 | -0.033523233207 |
| 7 | -41.812396798289 | -14.486504644254 | 6679.417677047104 | -0.006893683290 |
| 8 | -41.773458093352 | -16.745764141229 | 6375.894220189388 | -0.003271201156 |
| 9 | -41.772709847318 | -16.789178063878 | 6370.061714494449 | -0.003201591552 |
| 10 | -41.772709570934 | -16.789194106554 | 6370.059559223604 | -0.003201565830 |
Multivariate Newton's Method (*** STRESS TEST #4: Earth-Sun Distance = 92,960,000 miles = 149,604,618.24 km ***) |
||||
|---|---|---|---|---|
| Iteration | x | y | z | d |
| 0 | 0 | 0 | 149604618.24 | 0 |
| 1 | -9643.42968855 | 557080.26426601 | 74850372.48820066 | 893.24902974 |
| 5 | -640.927749755 | 34746.738450629 | 4676726.029667439 | -55.742817982 |
| 10 | -59.5337039432 | 1013.7200378651 | 144815.3000648108 | -1.6555134345 |
| 15 | -41.838768279149 | -12.956407051958 | 6884.980832217152 | -0.009347031919 |
| 16 | -41.774732646271 | -16.671813402899 | 6385.829238170562 | -0.003389773294 |
| 17 | -41.772711588080 | -16.789077063855 | 6370.075283488928 | -0.003201753495 |
| 18 | -41.772709570934 | -16.789194106436 | 6370.059559238973 | -0.003201565830 |
| 19 | -41.772709570896 | -16.789194106548 | 6370.059559223319 | -0.003201565830 |
| 20 | -41.772709570817 | -16.789194106513 | 6370.059559223363 | -0.003201565830 |
Part 2/3: Matlab "rref" ("Reduced Row Echelon Form" (Gauss-Jordan Elimination))
Gauss-Jordan Reduced Row Echelon Form Method Code (GaussJordanRREF.pdf)
Quadratic Equation |
|
|---|---|
| \[ -82854564582.53175240818981761143 * d^2 + 15077167846.761892504574543743006 * d + 49119806.64094493963509095287271 = 0 \] | |
Quadratic Solutions (2): One (1) Relevant *; One (1) Irrelevant: |
||||
|---|---|---|---|---|
| --- | 1 * | 2 | ||
| x | -41.7727095 | -39.7478373482 | ||
| y | -16.7891941065 | -134.274144361 | ||
| z | 6370.05955922 | 9413.62455374 | ||
Part 4: Satellite Positions in Spherical Coordinates
EMF Code (DriverEMFP4.m)EMF Code (ErrorMagnificationFactorP4.m)
EMF Calculations (outputP401.txt)
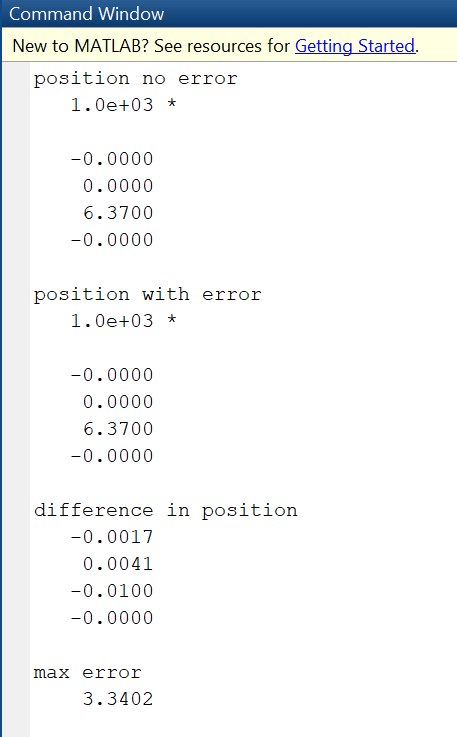
Part 5: Satellite Positions in Spherical Coordinates (Tightly Grouped Set of Satellites)
EMF Code (DriverEMFP5.m)EMF Calculations (outputP500.txt)

Part 6: Reduction in GPS Error and Condition Number by Adding Satellites
For Part 6, Matlab code was rewritten to allow for any number of unbunched satellites in a random grouping, as specified by $\phi$ and $\theta$ in Part 4. The following results were found for between 1 and 12 satellites:
Error vs. Number of Satellites |
||
|---|---|---|
| # Satellites | Relative Forward Error | Error Magnification Factor |
| 1 | 2.951193e+02 | 9.844119e+03 |
| 2 | 1.699170e+02 | 5.667820e+03 |
| 3 | 8.120928e-01 | 2.708850e+01 |
| 4 | 1.198875e-01 | 3.999018e+00 |
| 5 | 5.074772e-02 | 1.692762e+00 |
| 6 | 5.096588e-02 | 1.700039e+00 |
| 7 | 3.576615e-02 | 1.193030e+00 |
| 8 | 1.998035e-02 | 6.664728e-01 |
| 9 | 3.688600e-02 | 1.230385e+00 |
| 10 | 5.710890e-02 | 1.904948e+00 |
| 11 | 5.778053e-02 | 1.927351e+00 |
| 12 | 2.573939e-02 | 8.585736e-01 |
Based on the above results, compared with the results from Parts 4 and 5, 8 satellites unbunched result in the best possible error magnification factor. Notably, however, diminishing returns were seen after 5 or more unbunched satellites were added. That being said, error still generally decreased as more satellites were added, with 8 being particulary low in error in this case.
Part 7: Improvement of Error Magnification Factor Moving Toward Horizon
When working on problem 5 we stumbled on an interesting problem. We had already run into an issue in problem 4 that if we were to put a satellite directly over the north pole or close to the north pole we would have an error that could put you on mars. In problem 5 we found that as we moved our cluster down from the north pole to the horizon we continuously found a smaller error until we hit a floor of about 35 for our max error. We also discover that if you set either the phi or theta to be the same for of the satellites while leaving the other within 5% we see the error grown back to several million. We came to the conclusion that setting all of the satellites in a line (a product of keeping the phi or theta constant) that the satellites would be read as the same causing a problem with our system of equations.
********************** BELOW-THE-LINE ******************************************** **********************************************************************************