function eigenfaces()
n=40;
dim = 112*92;
x = zeros(dim,n);
for i=1:n
x(:,i) = reshape(double(imread(strcat('train/s', num2str(i), '.1.tif'))), [dim 1]);
end
m = mean(x,2);
x = bsxfun(@minus, x, m);
[U,S,V] = svd(x);
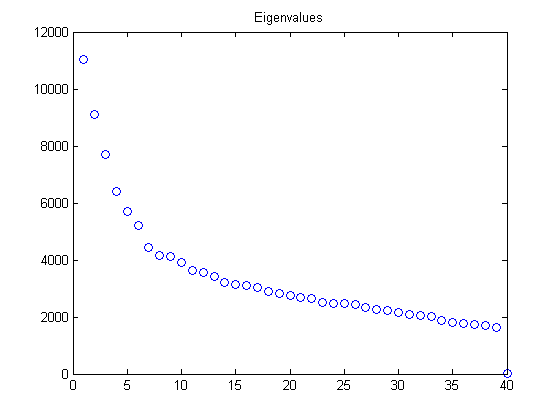
figure; plot(diag(S), 'bo'); set(gcf, 'color','w'); title('Eigenvalues');
figure; set(gcf, 'color', 'w'); title('8 best eigenfaces');
for i=1:8
subplot(2,4,i); imshow(reshape(U(:,i), [112,92]), []);
end
E = U(:,1:8);
W = E'*x;
y = zeros(dim,n);
for i=1:n
y(:,i) = reshape(double(imread(strcat('test/s', num2str(i), '.2.tif'))), [dim 1]);
end
y = bsxfun(@minus, y, m);
Z = E'*y;
matches = zeros(1,40);
for i=1:40
minDistance = Inf;
index = 0;
for j=1:40
distance = norm(Z(:,i) - W(:,j));
if distance < minDistance
minDistance = distance;
index = j;
end
end
matches(i) = index;
end
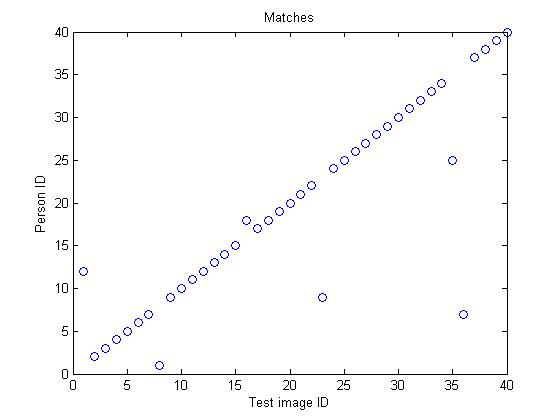
figure; plot(matches, 'bo'); set(gcf, 'color','w'); title('Matches');
xlabel('Test image ID'); ylabel('Person ID');
end