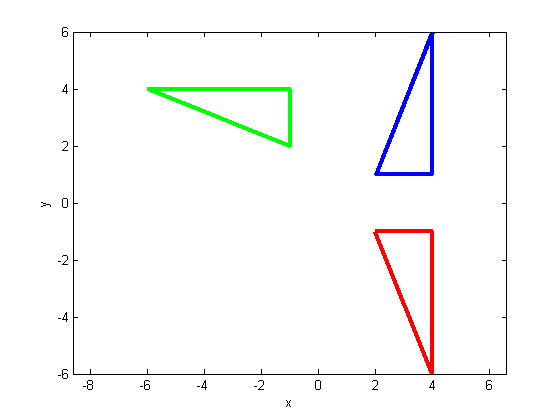
% Triangle (repeating points allow it to be plotted)
tr = [2,1; 4,1; 4,6; 2,1]';

% Plot the original triangle in blue
plot(tr(1,:), tr(2,:), 'b', 'LineWidth', 3);
set(gcf, 'color', 'w')
xlabel('x')
ylabel('y')
axis equal;
hold on;

% Let the angle of rotation be 90degrees
theta = 90;

% The first rotation matrix
T1 = [cosd(theta), -sind(theta);
      sind(theta), cosd(theta)];

% Determinant is 1
disp(strcat('det(T1)=', num2str(det(T1))));

% Triangle rotated with T1 plotted in green
tr1 = T1*tr;
plot(tr1(1,:), tr1(2,:), 'g', 'LineWidth', 3);
hold on;

% The second rotation matrix
T2 = [sind(theta), cosd(theta);
      cosd(theta), -sind(theta)];

% Determinant is -1
disp(strcat('det(T2)=', num2str(det(T2))));

% Triangle rotated with T2 plotted in red
tr2 = T2*tr;
plot(tr2(1,:), tr2(2,:), 'r', 'LineWidth', 3);

% COMMENTS:
% T2 is NOT a rigid body transformation because it does not preserve the
% orientation of the triangle. The difference between T1 and T2 is that
% the x-axis and the y-axis are switched, which turns the normal
% (right-handed) coordinate system into a left-handed one. If we imagine
% the triangle as a tile, T2 requires us to flip the tile upside down,
% thus leaving the plane of rotation.

det(T1)=1
det(T2)=-1