Mauro Rubio's 447 Projects
Project 3
Partner:Step 1
Here we have to write a program in Matlab that uses adaptive quadrature to compute the arc length from t = 0 to t = T for a given T ≤ 1. For this we used Length = adapquad(fnew,0,T,tol0) with tol0 = 10-8. See project3step1.m for code.
Step 2
Step 2 asks us to write a program in Matlab that for any input s between 0 and 1, finds the parameter t*(s) that is s of the way along the curve. This means that the arc length from t = 0 to t = t*(s) divided by the arc length from t = 0 to t = 1 should equal to s. We used the Bisection Method to locate the point t*(s) to three correct decimal places. See project3step2.m for code.
For the Bisection Method we used a staring interval of [-10,10]. Starting with an initial guess of 1 we have>> project3step2(1)
ans = 0.999984741210938
Step 3
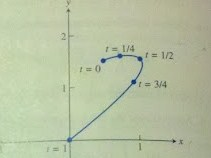
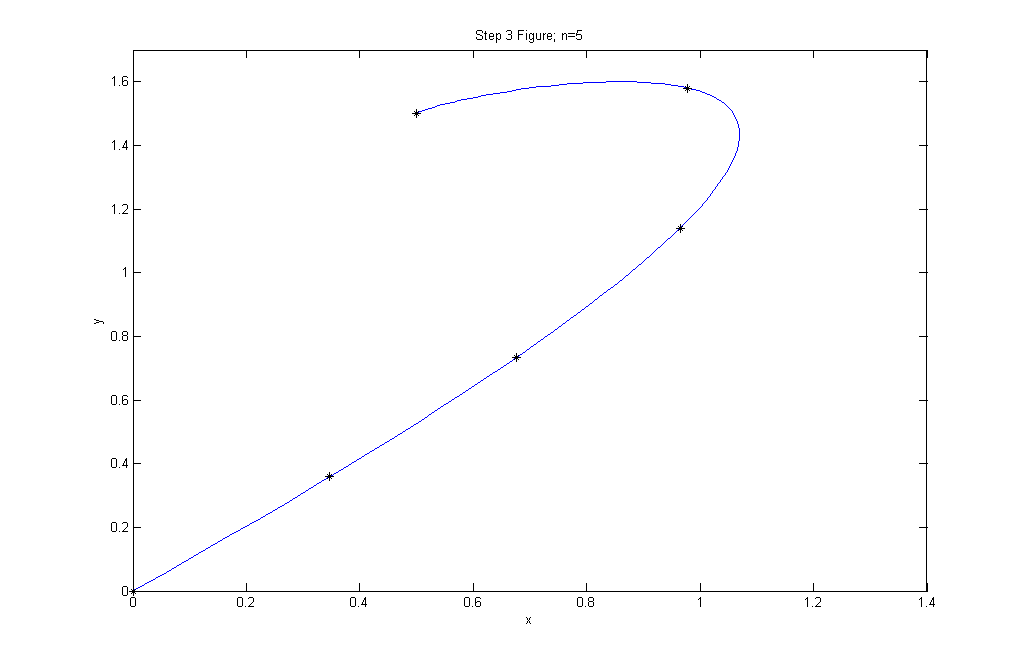
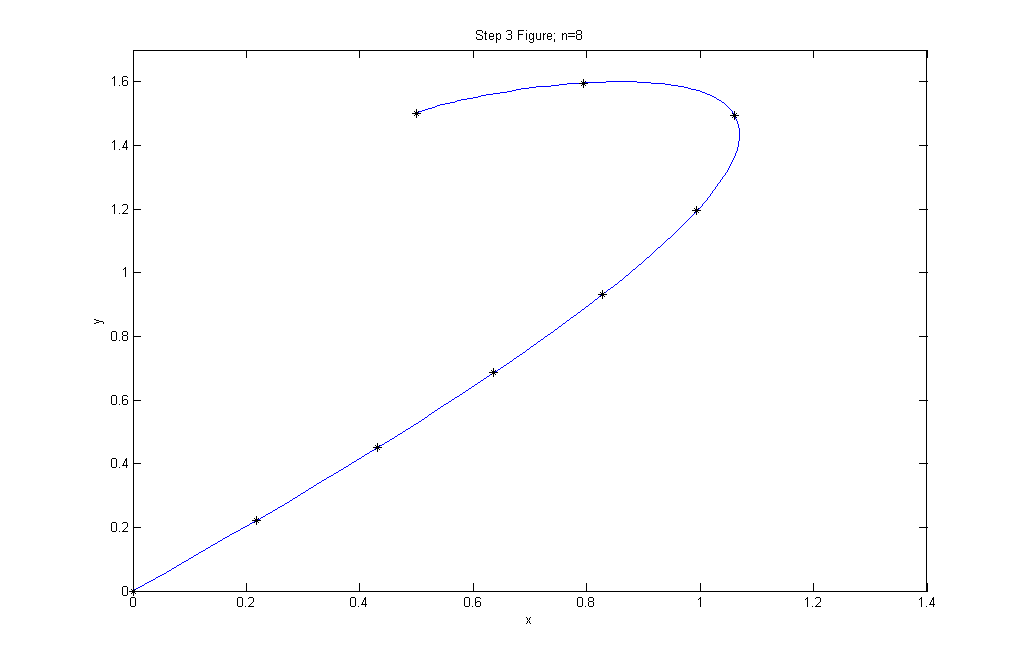
Step 3 asks us to equipartition the path shown in Figure 5.6 (pg 280) into n subpaths of equal length; we used n = 5 and n = 8. Code for n=5 and n=8
Step 4
Here we replace the Bisection Method in Step 2 with Newton's Method, and repeated Steps 2 and 3. See project3step42.m for code for Step 2 done with Newton's Method. See project3step43.m for code for Step 3 done with Newton's Method.
Step 5
In Step 5 we used Matlab's animation commands to demonstrate traveling along the path, first at the original parameter 0 ≤ t ≤ 1 speed and then at the constant speed given by t*(s) for 0 ≤ s ≤ 1.Step 6
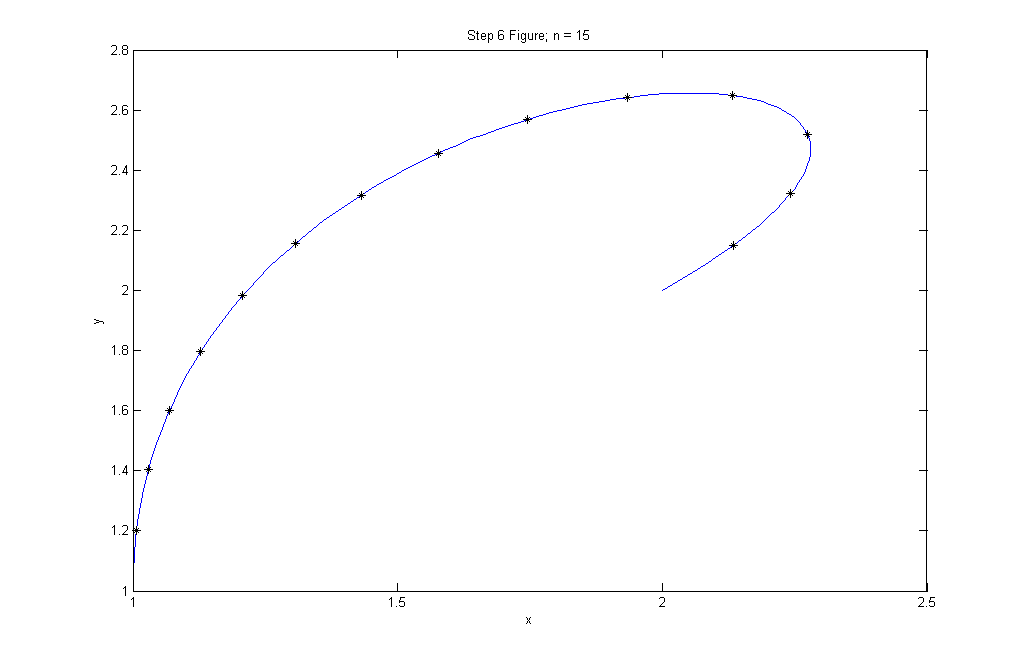
Here we experimented with equipartitioning a path of our choice into n segments. Here is the code for Step 6 project3step6.m.
We used the points (x1,y1)=(1,1),(x2,y2)=(1,3),(x3,y3)=(3,3),(x4,y4)=(2,2) to obtain our Bezier curve:x(t) = 1+6*t2-15*t3
y(t) = 1+6*t-6*t2+t3
We partitioned the path using n=15