Mauro Rubio's 447 Projects
Project 2
Partner: Shelby Doolittle. To see Shelby's webpage for Project 2, click:GPS is a system used by millions to navigate their world and has been used to save the lives of hikers lost in the wilderness. The system consists of 24 satellites positioned 20200 km above the earth's surface. These satellites send out precisely timed signals that are picked up by GPS receivers on the ground. These receivers use the times from the satellites and their location to determine the position of the receiver. Because of the inaccuracy of the clock in the receiver, four satellites are needed to calculate the position in three dimensions and the error in the receiver time.
Ideally, if we had the proper x, y, z, and difference in time, d, for the receiver, then the following equations would be zero:
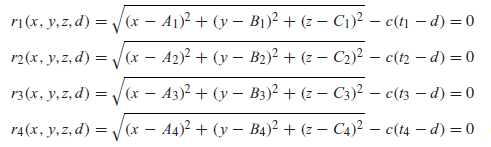
Equation 1
Where c is the speed of light, approximately c = 299,792.458 km/s, and A, B, C, and t are the x position, y position, z position, and time received from each of the four satellites, respectively. We can use some algebra to solve this system directly for x, y, z, and d. This is explained in Problem 1 below.
Once this step is completed we have 3 equations and 4 unknowns. Our next step is to set up the matrix equation
x(Ux)+y(Uy)+z(Uz)+d(Ud)+W=0. Where each Ui and W are obtained from the subtracting method explained above. Once this is done, we take the determinant on each vector to obtain an equation interms of d that we can then substitute into the
first equation in Equation 1. We can then find what the time correction d is for the given input values. Using the code in
Number1CodeProject2.m we get d= -0.003201565829594 , 0.185173047095946 CurrrentLocation = 1.0e+003 * -0.041772709570836 , -0.039747837348212 -0.016789194106525 , -0.134274144360690 6.370059559223342 , -9.413624553735811 The column on the right-hand side is discarded as it does not lie on
the surface of Earth; it is way out in space. This column corresponds the
other intersecting point of the three spheres. Alternatively, we can use a variation of Newton's Method to solve this iteratively. Recall Newton's Method:
In this case our functions are the ones in Equations 1, represented in
f.m Problem 1.)
Using Matlab code Number1CodeProject2.m
we were able to find the reciever position (x,y,z) near Earth and time correction d for the four known satellite positions and
their measured time intervals. The time correction d is the difference between the synchronized time on the four satellite clocks and
the Earth-bound reciever (the GPS device) clock.
In doing the calculations to figure out the correct d for the four satellites, we subtracted the last three equations from the first in
an attempt to get an equation in terms of only the variable d.
Problem 3.)
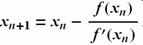
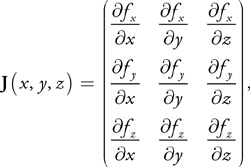
We use getlocation.m to calculate the location of the receiver given a matrix of satellite positions and times.
Passing this as an argument to getlocation.m, we calculate the x, y, z to be (-41.77271, -16.78919, 6370.0596) and d = -.003201566, which agrees with the calculation from the algebra.
Now we can inspect the error in the system. The satellite transmission has to travel through 100 km of atmosphere which can affect the transmission speed. This rarely affects the time more than 10 nanoseconds. The file testsats.m will test a group of satellites for the maximum possible error. It assumes the receiver is at (0,0,6370) with d = 0.0001. It then calculates the times that each satellite should transmit given their location. We then iterate through all possible changing of each of those times by either adding or subtracting 10-8 seconds or not changing it. It then returns the maximum error magnification given by the greatest error in x, y, or z divided by c*10-8.
Next, we can use the file metatest.m to produce a random set of a given number of satellites and run testsats.m to inspect the type of error we get with that number of satellites. Finally, we use bigmeta.m to run metatest.m with different numbers of satellites and compute the mean and standard deviation of each number. Due to computing limits (because this system grows exponentially, with n+1 satellites taking 3 times as long as n) we were limited to only inspecting 100 random sets of satellites for 4, 5, 6, 7, and 8 satellites. The following logarithmic base 10 graph plots the number of satellites versus the mean as blue dots, one standard deviation in the positive direction as green dots and the blue line, and one standard deviation in the negative direction as red dots and the green line.
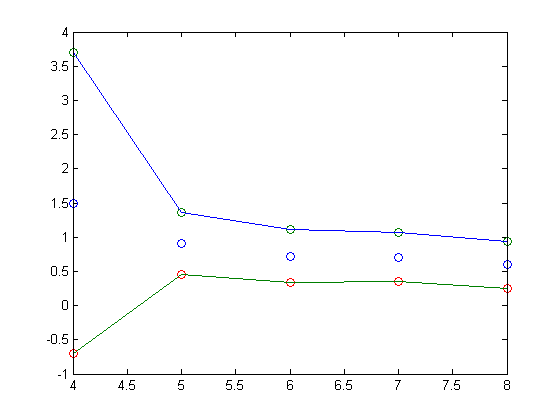
With four satellites, the output error is on the order of 31 times the input error, corresponding to approximately a 92 meter error, while varying wildly. Increasing to eight satellites, the error drops drastically to a relatively small 4 times the input error, corresponding to only 11 meters.
We can see that the GPS system we have implemented is not accurate enough to differentiate between two streets in a city with merely four satellites. Gladly, the designers realized this problem and made sure that at any time and location 5 to 12 satellites are visible, drastically increasing the accuracy. Since these errors are the worst case scenario for a given set of satellites, we expect the error in practice to rarely reach levels this severe.